AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tangent at C intersects AB extended at D, then BC=BD.
A circle is drawn with center O and AB is a diameter
AC is a chrod such that ∠BAC=30∘.
Given AB is ∝ diameter and AC is a chord of circle with centre O, ∠BAC=30∘.
To prove BC=BD

Proof ∠BCD=∠CAB [alternate segment theorem]
∠CAB=30∘ [given]
∴∠BCD=30∘.....(i)
In ΔABC,∠ACB=90∘ [angle in semi-circle is right angle]
∠A+∠B+∠C=180∘
30∘+∠B+90∘=180∘
⇒∠B=60∘
Also, ∠CBA+∠CBD=180∘ [linear pair]
⇒∠CBD=180∘−60∘−120∘ [∵∠CBA=60∘]
Now, in ΔCBD
∠CBD+∠BDC+∠DCB=180∘
⇒120∘+∠BDC+30∘=180∘ [from Eq. (i)]
⇒∠BDC=30∘⇒∠BDC=30∘.....(ii)
From Eqs. (i) and (ii),
∠BCD=∠BDC
∴BC=BD
[sides opposite to equal angles are equal]
Topper's Solved these Questions
Similar Questions
AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tangent at C intersects AB extended at D, then BC=BD.
View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View Solution
Knowledge Check
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
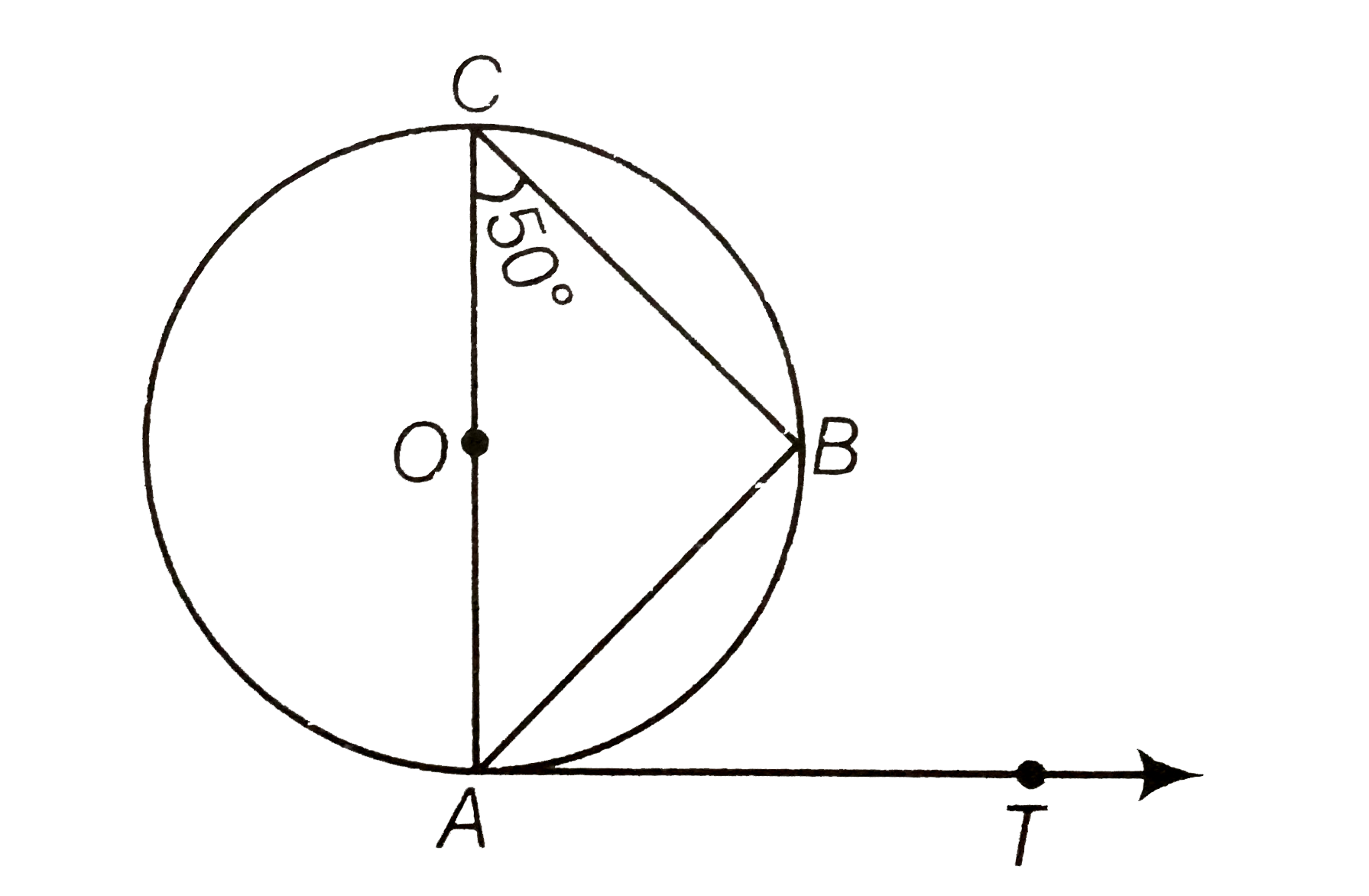 A45∘B60∘C50∘D55∘
A45∘B60∘C50∘D55∘AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
A30∘B60∘C90∘D45∘
AB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD = AB. The tangent at B meets the line AC produced at E then AE is equal to
View SolutionIf AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
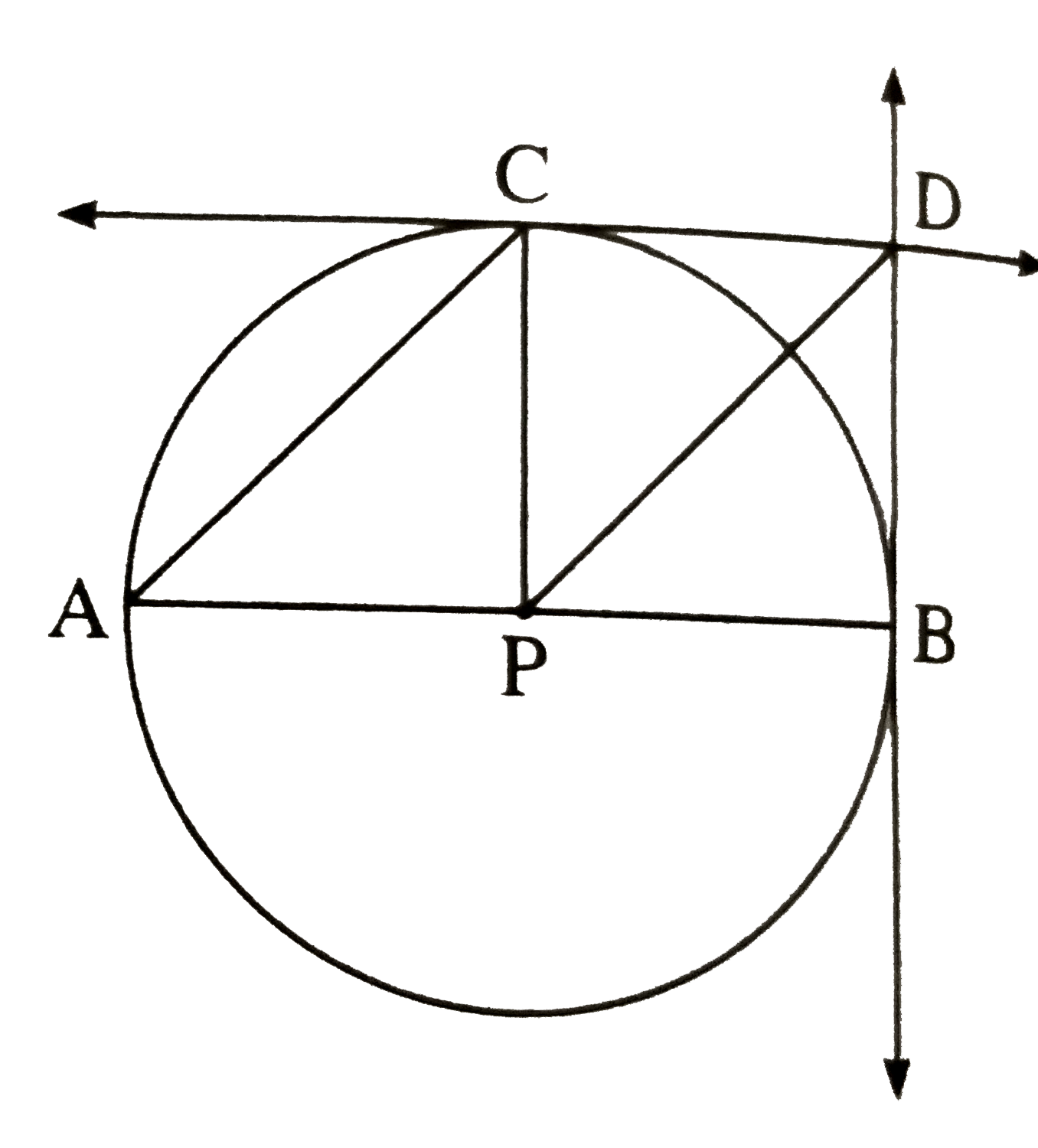
View SolutionAB is diameter of a circle with centre 'O'. CD is a chord which is equal to the radius of the circle. AC and BD are extended so that they intersect each other at point P. Then find the value of ∠APB.
View SolutionAB is the diameter of a circle whose centre is O. DC is a chord of that circle. If DC||AB and ∠BAC=20∘ then ∠ADC=?
View Solution
