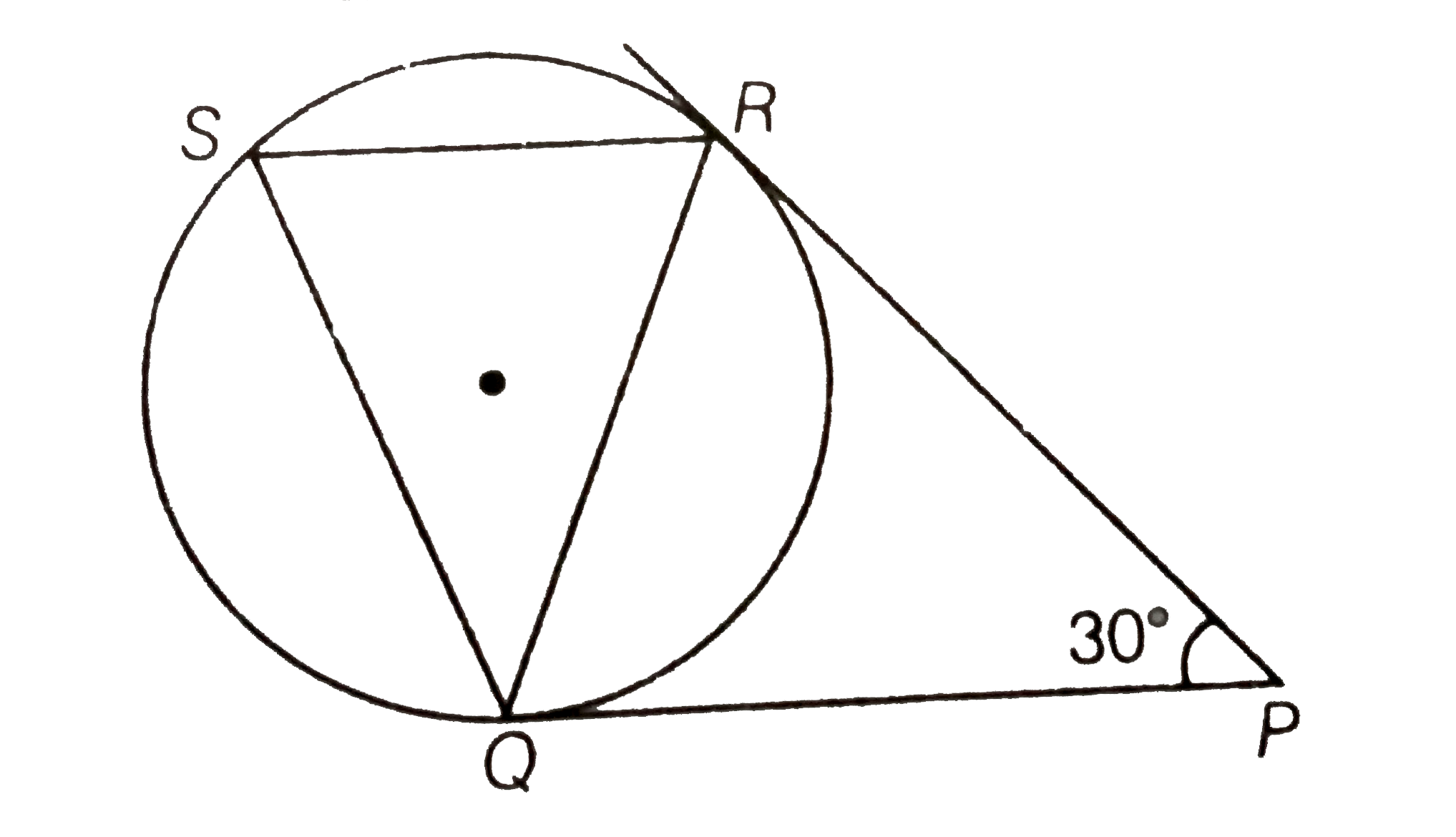
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ=30∘. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
30∘
40∘
50∘
60∘
The correct Answer is:A
PQ and PR are two tangents drawn from an external point P.

∴PQ=PR
[the lengths of tangents drawn from an external point to a circle are equal]
⇒∠PQR=∠QRP
[angles opposite to equal sides are equal]
Now, in ΔPQR ∠PQR+∠QRP+∠RPQ=180∘
[sum of all interior angles of any triangle is 180∘]
⇒∠PQR+∠PQR+30∘=180∘
⇒2∠PQR=180∘−30∘
⇒∠PQR=180∘−30∘2=75∘
Since, SR/QP
∴∠SRQ=∠RQP=75∘ [alternate interior angles]
Also, ∴∠PQR=∠QSR=75∘ [by alternate segment theorem]
In ΔQRS,∠Q+∠R+∠S=180∘
[sum of all interior angles of any triangle is 180∘]
⇒∠Q=180∘−(75∘+75∘)
=30∘
∴∠RQS=30∘
Topper's Solved these Questions
Similar Questions
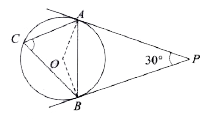
In Figure, if tangents PAandPB are drawn to a circle such that ∠APB=300 and chord AC is drawn parallel to the tangent PB, then ∠ABC= 600 (b) 900 (c) 300 (d) None of these
View SolutionTangents AB and AC are drawn to a circle from a point A, such that ∠BAC=40∘. A chord CP is drawn parallel to BA. The measure of ∠CBP is:
View Solution
Knowledge Check
In figure , tangents PA and PB are drawn to a circle such that ∠APB=30∘ and chord AC is drawn parallel to the tangent PB then ∠ABC=
 A60∘B50∘C30∘Dnone of these
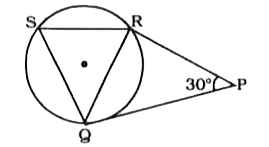
A60∘B50∘C30∘Dnone of theseIn the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPO=30∘. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
 A30∘B50∘C45∘D60∘
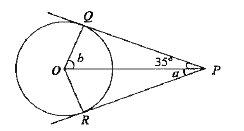
A30∘B50∘C45∘D60∘In the figure , PQ and PR are the tangents drawn form P to a circle with centre O. if ∠OPQ=35∘ then
 Aa=30∘,b=60∘Ba=35∘,b=55∘Ca=40∘,b=50∘Da=45∘,b=45∘
Aa=30∘,b=60∘Ba=35∘,b=55∘Ca=40∘,b=50∘Da=45∘,b=45∘
In the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionIn Figure, common tangents PQandRs to two circle intersect at A. Prove that PQ=RS.
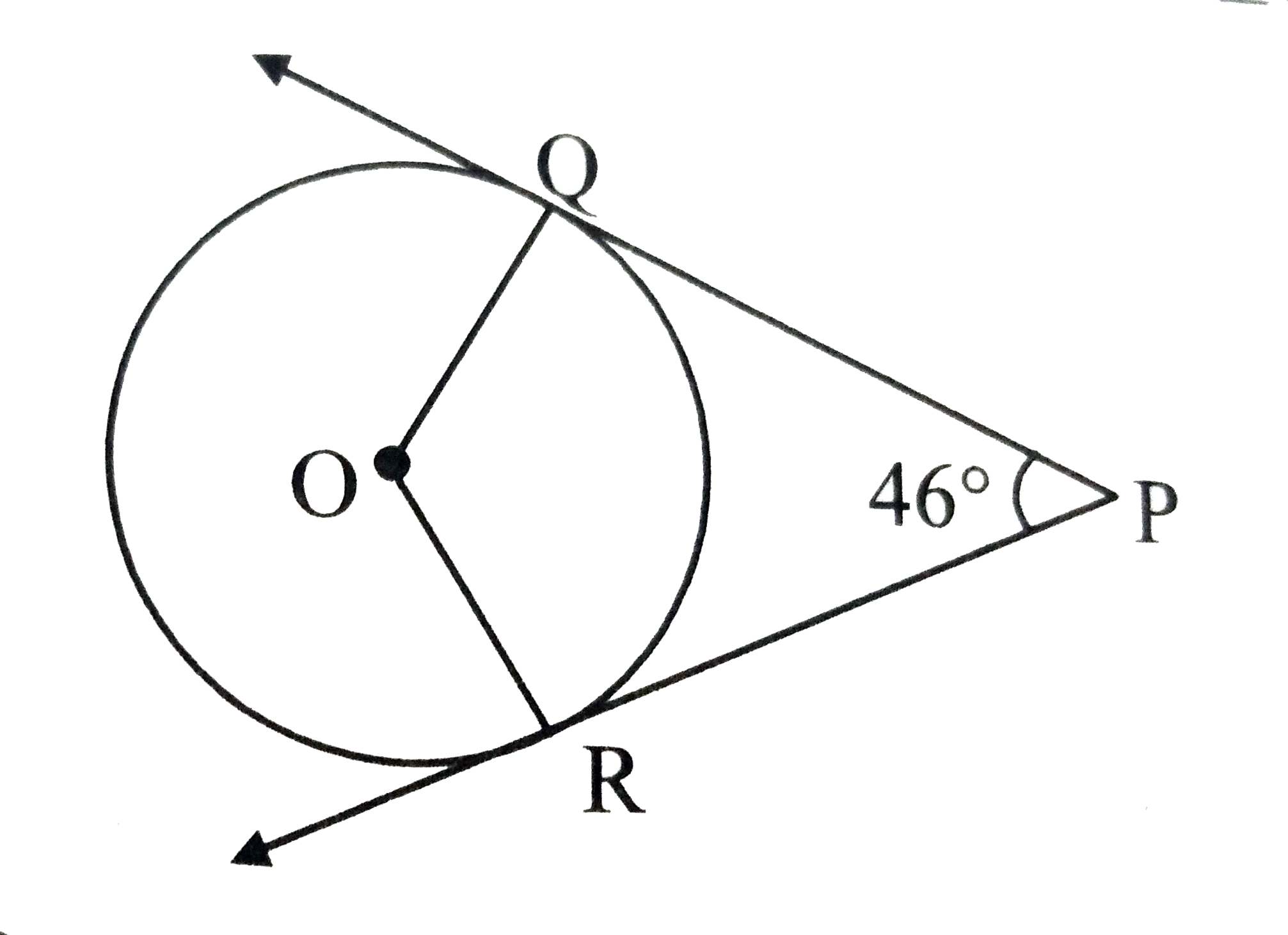
View SolutionIn figure, PQ and PR are two tangents to a circle with centre O. IF ∠QPR=46∘ , then ∠QOR equals
View SolutionIf Figure-1, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. if ∠QPR=90∘, then length of PQ is
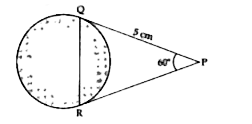
View SolutionIn the give figure ,PQ and PR are tangents to the given circle such that PQ =5 cm and ∠QPR=60∘. The length of chord QR is
View Solution
