A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle,Prove that R bisects the arc PRQ.
Video Solution
Text Solution
Given Chord PQ is parallel to tangent at R.
To prove R bisects the are PRQ
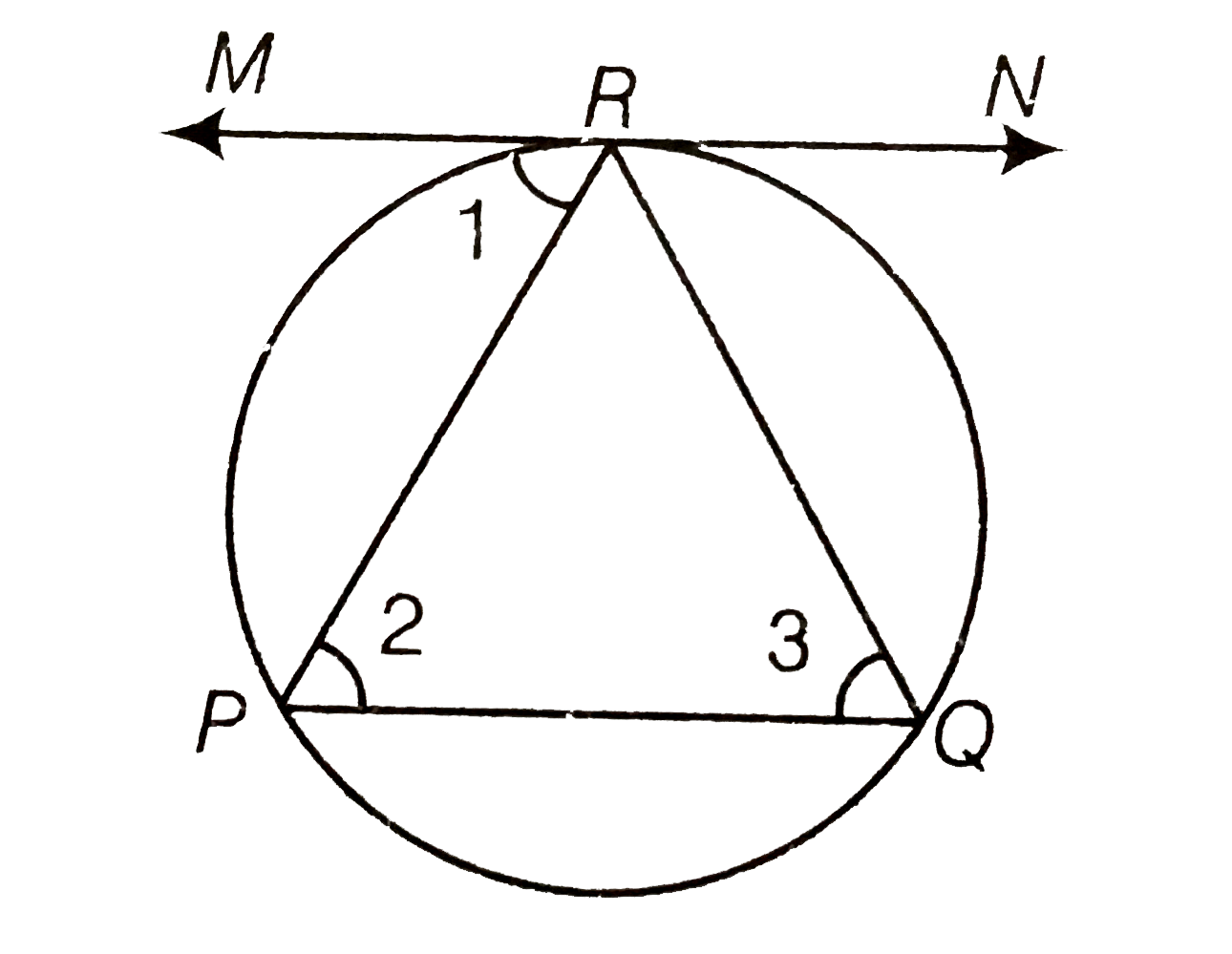
Proof ∠1=∠2 [alternate interior angles]
∠1=∠3
[angle between tangent and chord is equal to angle made by chord in alternate segment]
∴∠2=∠3
⇒PR=QR [sides opposite to equal angles are equal]
⇒PR=QR
So, R bisects PQ.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A circle with radius r has a chord PQ whose length is 2a. The tangents drawn at points PandQ to the circle meet at T, what is the length of TP?
Aar√r2−a2B2ar√r2−a2Cr2+a2√r2−a2Darr−aIf the length of a chord of a circle , which makes a angle 45∘ with the tangent drawn at one end point of the chord , is 6 cm , then the radius of the circle is :
A6√2 cmB5 cmC3√2 cmD6 cmA chord of a circle is equal to its radius. A tangent is drawn to the circle at an extremity of the chord. The angle between the tangent and the chord is
A30∘B45∘C60∘D75∘
Prove that the length of the tangents drawn from an external point to a circle are equal.
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
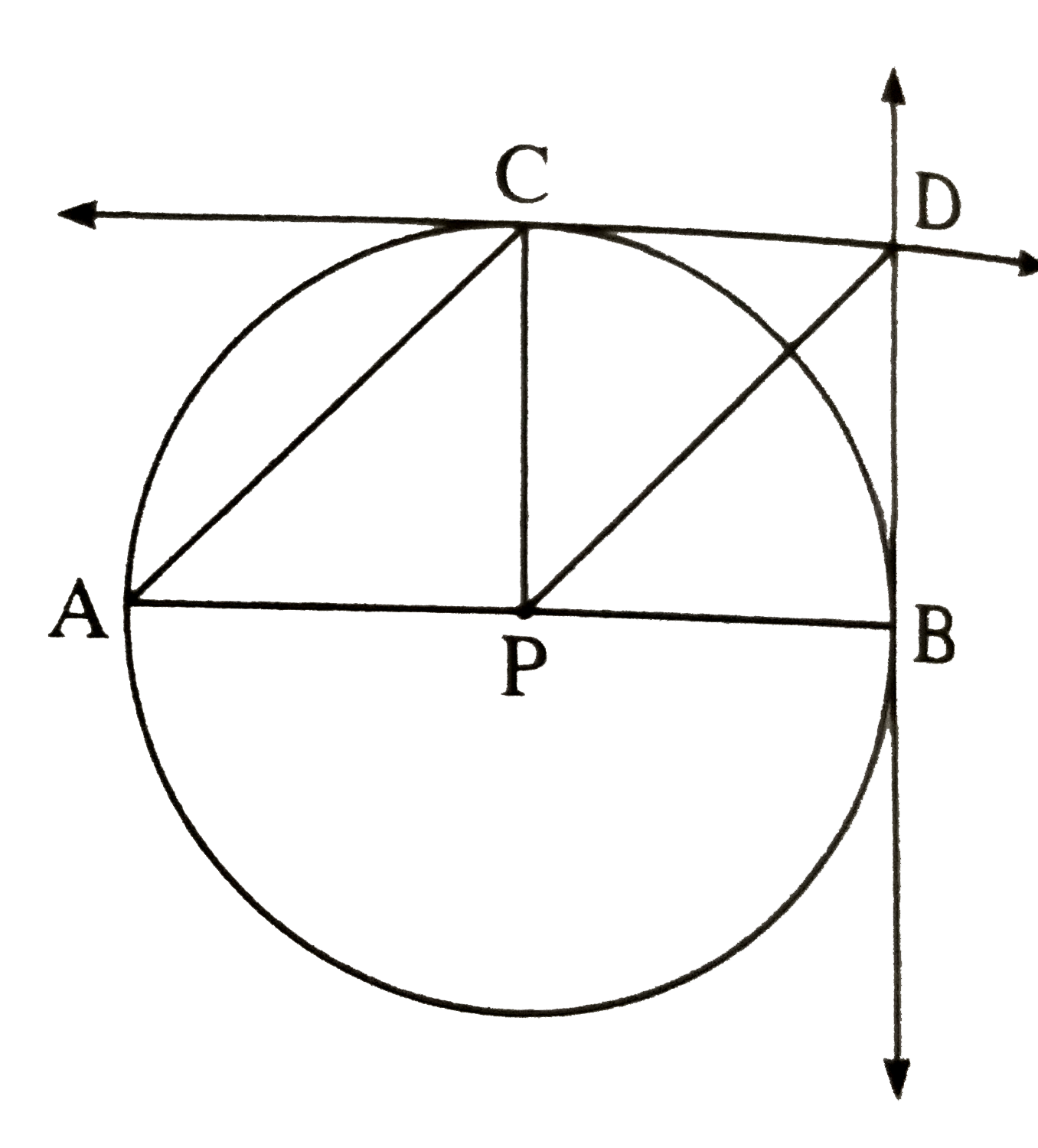
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionTangents are drawn at extremities AB of a diameter of a circle centred at P. If tangents drawn at a point C on the circle meet the other two tangents respectively at Q and R then measure of ∠QPR is
View Solution
