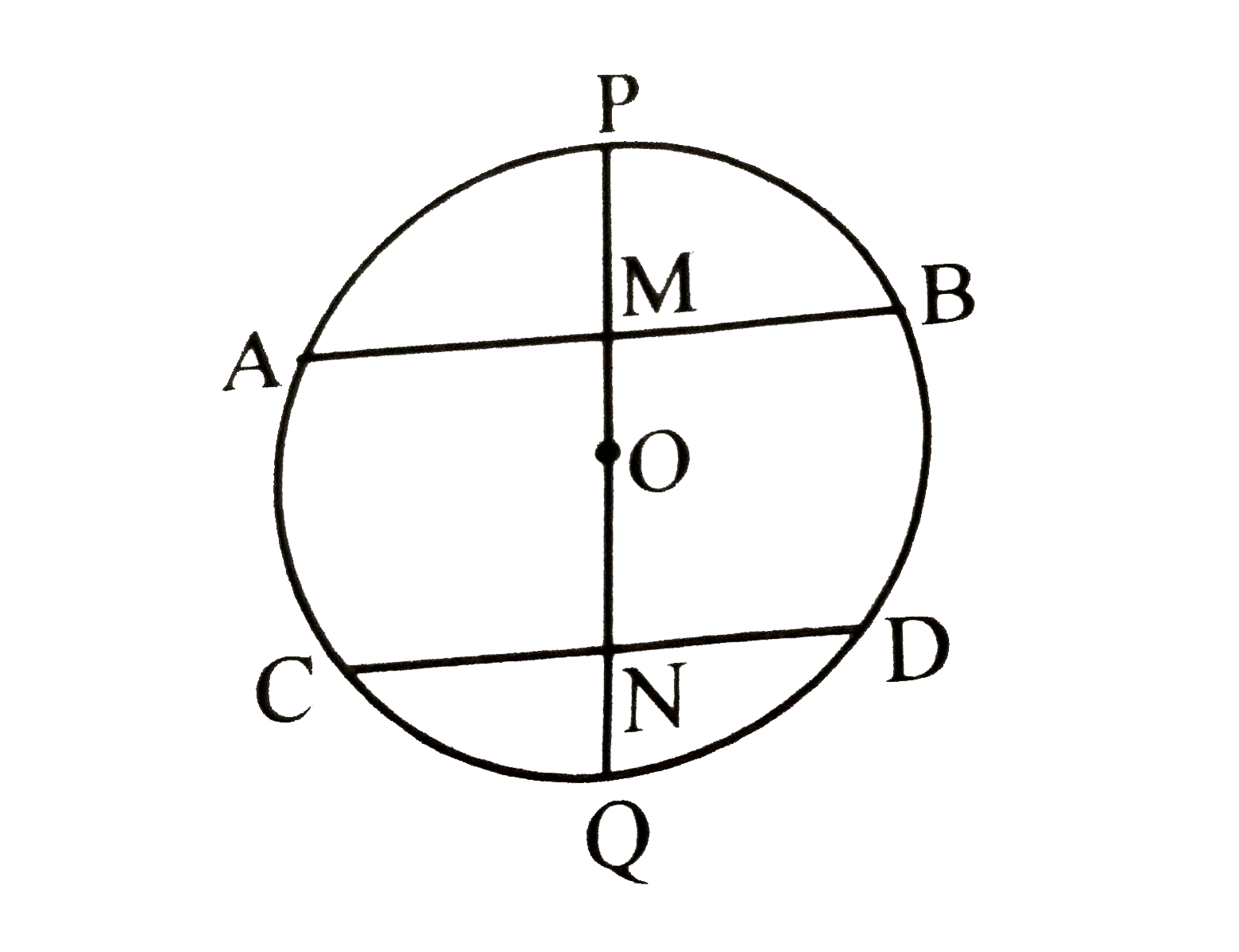
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Given, AB is a diameter of the circle.
A tangent is drawn from point A. Draw a chord CD parallel to the tangent MAN.

So, CD is a chord of the circle and OA is a radius of the circle.
∠MAO=90∘
[tangent at any point of a circle is perpendicular to the radius through the point of contact]
∠CEO=∠MAO [corresponding angles]
∴∠CEO=90∘
Thus, OE bisects CD, [perpendicular from centre of circle to the radius through the point of contact]
Similarly, the diameter AB bisects all. Chords which are parallel to the tangent at the point A.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The tangents are drawn at the extremities of diameter AB of a circle with centre P. If a tangent to the circle at the point C Intersects the other two tangents at Q and R, then the measure of the ∠QPR is
A45∘B60∘C90∘D180∘
If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD = AB. The tangent at B meets the line AC produced at E then AE is equal to
View SolutionIn the given figure, a diameter PQ of a circle bisects the chord RS at the point O. If PS is parallel to RQ, prove that RS is also a diameter of the circle.
View SolutionCircle described on the focal length as diameter touches the tangent at the vertex
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View Solution