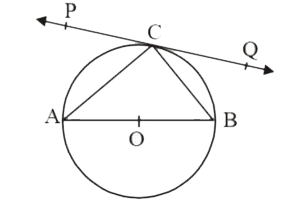
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA=110∘find∠CBA.
A
20∘
B
70∘
C
60∘
D
80∘
Video Solution
Text Solution
The correct Answer is:B
Here, AB is a diameter of the circle from point C and a tangent is drawn which meets at a point P.

Join OC. Here, OC is radius.
Since, tangent at any point of a circle is perpendicular to the radius through point of contact circle.
OC⊥PC
Now, ∠PCA=110∘ [given]
⇒∠PCO+∠OCA=110∘
⇒90∘+∠OCA=110∘
⇒∠OCA=20∘
∴OC=OA=Radius of circle
⇒∠OCA=∠OAC=20∘
[since, two sides are equal, then their opposite angles are equal]
Sicne, PC is a tangent, so ∠BCP=∠CAB=20∘
[angles in a alternate segment are equal]
In ΔPBC,∠P+∠C+∠A=180∘
∠P=180∘−(∠C+∠A)
=180∘−(110∘+20∘)
180∘−130∘=50∘
In ΔPBC,∠BPC+∠PCB+∠PBC=180∘
[sum of all interion angles of any triangle is 180∘]
⇒50∘+20∘+∠PBC=180∘
⇒∠PBC=180∘−70∘
⇒∠PBC=110∘
Since, APB is a straight line.
∴∠PBC+∠CBA=180∘
⇒∠CBA=180∘−110∘=70∘
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
AB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?A5∘B7∘C17∘D6∘The tangent at a point A of a circle with centre O intersects the diameter PQ of the circle (when extended) at the point B. If ∠BAP=125∘, then ∠AQP is equal to :
A45∘B55∘C60∘D50∘The tangent at a point A on a circle with center O intersects the diameter PQ of the circle, when extended,at point B. If ∠BAQ=105∘, then ∠APQ is equal to:
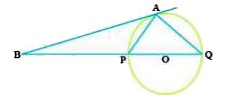 A55∘B60∘C65∘D75∘
A55∘B60∘C65∘D75∘
In 2, PQ is a tangent at a point C to circle with centre O. If AB is a diameter and ∠CAB=30∘ then find ∠PCA.

View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 110∘ , find ∠POA.
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionDraw the tangent to a circle of diameter 4 cm at a point P on it.
View SolutionAB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
View Solution