In figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.

Video Solution
Text Solution
Given AB and CD are tangents to two circles of equal radii.
To prove AB=CD
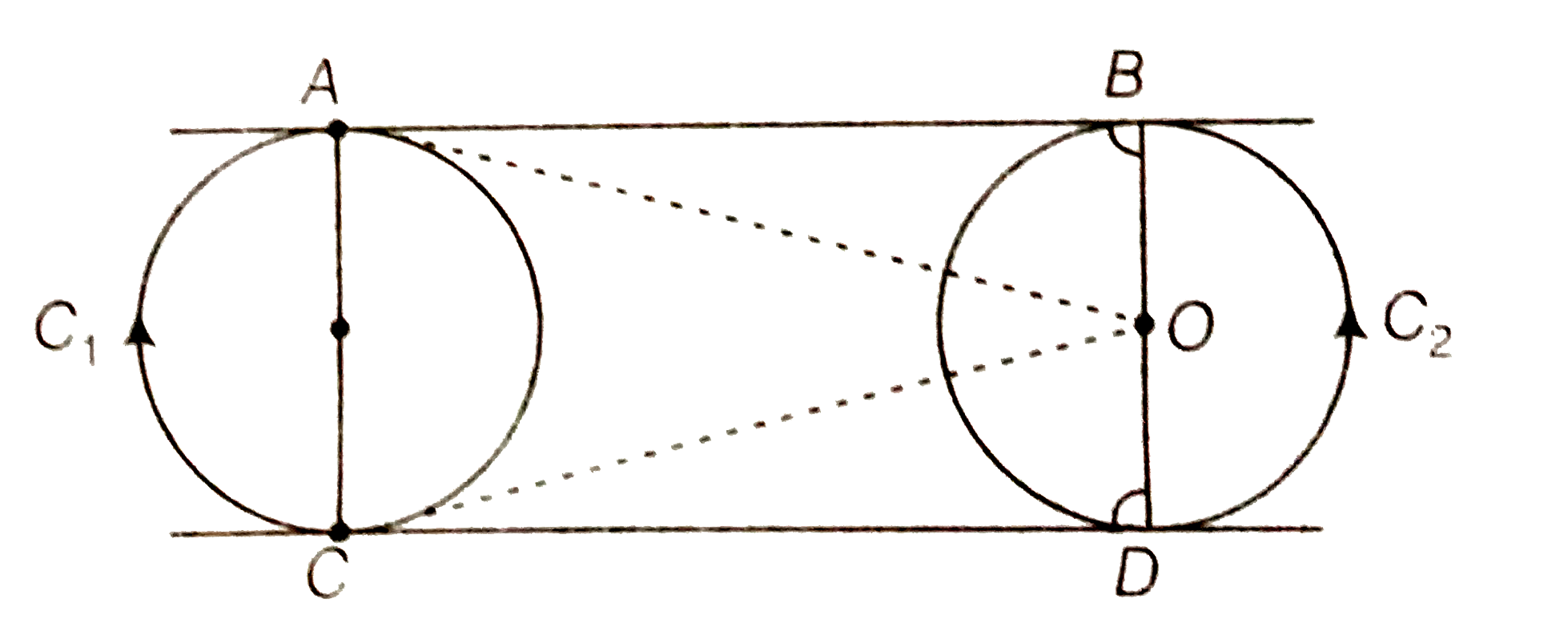
Construction Join OA, OC, O' B and O'D
Proof Now, ∠OAB=90∘
[tangent at any point of a circle is perpendicular to radius through the point of contact]
Thus, AC is a straight line.
Also, ∠OAB+∠OAB=180∘
∴AB/CD
Similarly, BD is a straight line
and ∠O'BA=∠O'DC=90∘
Also, AC=BD [radii of two circles are equal]
In quadrilateral ABCD, ∠A=∠B=∠C=∠D=90∘
and AC=BD
ABCD is a rectangle
Hence, AB=CD [opposite sides of rectangle are equal]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, AB||CD then
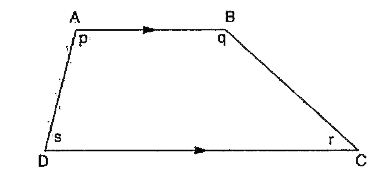 Ap+r=q+sBp−r=q−sCp+s=q+rDp−q=s−r
Ap+r=q+sBp−r=q−sCp+s=q+rDp−q=s−rIn the given figure, AB and CD are two common to the two touching circle. If CD=6cm, then AB is equal to
 A9 cmB15 cmC12 cmDnone of the above
A9 cmB15 cmC12 cmDnone of the above
In the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.

View SolutionCommon tangents AB and CD to two circles intersects at E. Prove that AB=CD
View SolutionAB and CD are common tangents to two circles which intersect each other at C as shown in the figure IF AB = 6cm , find CD.

View SolutionAB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD.
View SolutionAB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD
View SolutionIn the given figure,AB and CDare equal chords of a circle with centre O .Prove that ∠AOB≅∠COD and ∠AOB=∠COD
View Solution

