Two circles with centers O and O' of radii 6cm and 8 cm respectively intersect two points P and Q such that OP and O'P are tangents to the two circle. The length of the common chord PQ is

Video Solution

Text Solution

Verified by Experts

Here, two circles are of radii OP=3cm and PO'=4cm.
These two circles intersect at P and Q.

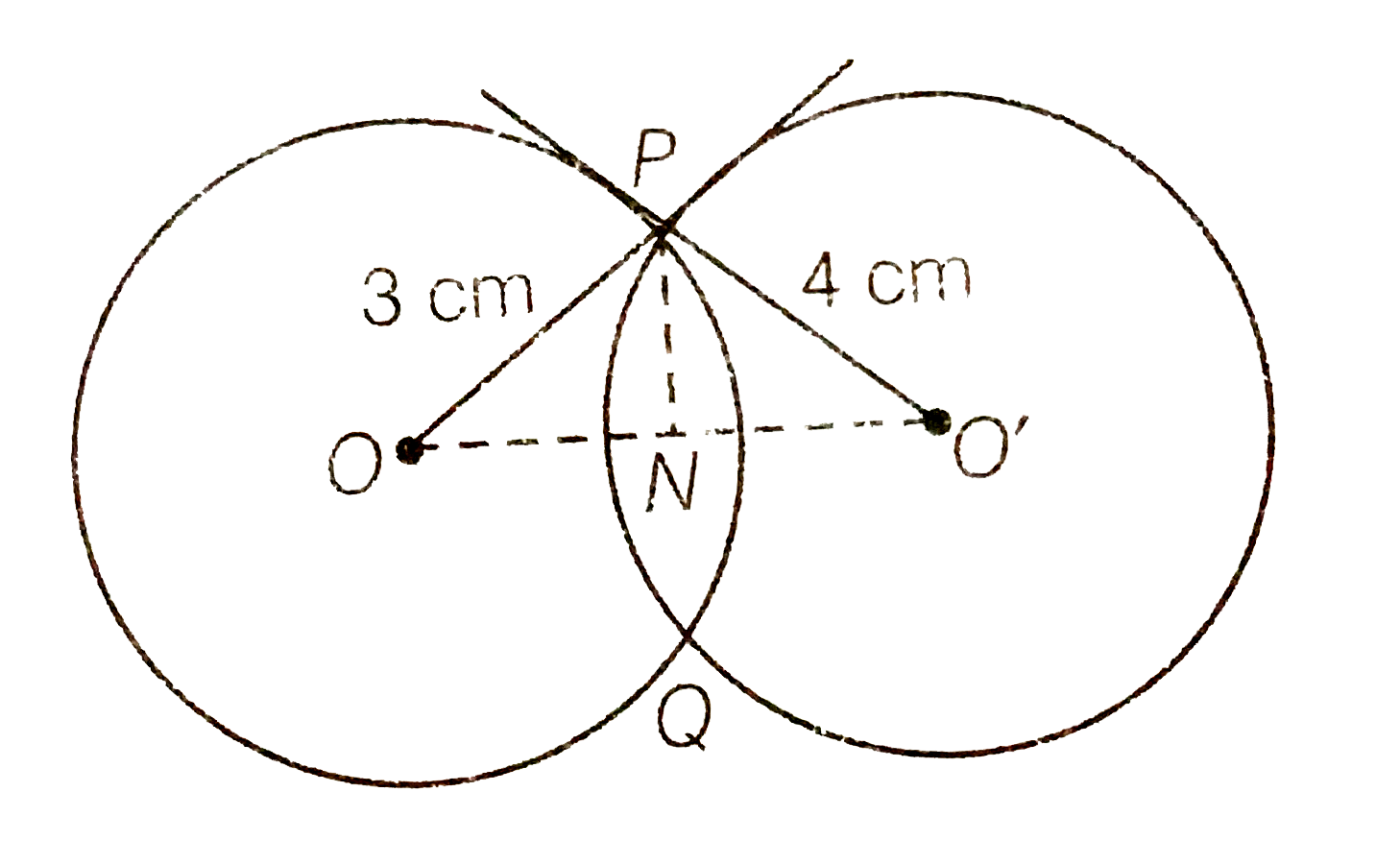
Here, OP and PO' are two tangents drawn at point P.
$∠ O P O' = 90^{\circ}$
[tangent at any point of circle is perpendicular to radius through the point of conctact]
Join OO' and PN,
In right angled $Δ O P O'$ ,
${(O O')}^{2} = {(O P)}^{2} + {(P O')}^{2}$ [by Pythagoras theroem]
i.e., ${(Hypotenuse)}^{2} = {(Base)}^{2} + {(Perpendiu lar)}^{2}$
$= {(3)}^{2} + {(4)}^{2} = 25$
$\Rightarrow O O' = 5 c m$
Also, $P N ⊥ O O'$
In right angled $Δ O P N$
${(O P)}^{2} = {(O N)}^{2} + {(N P)}^{2}$ [by Pythagoras theorem]
$\Rightarrow {(N P)}^{2} = 3^{2} - x^{2} = 9 - x^{2} ... ... (i)$
and in right angled $Δ P N O'$ ,
${(P O)}^{2} = {(P N)}^{2} + {(N O')}^{2}$ [by Pythagoras theorem]
${(4)}^{2} = {(P N)}^{2} + {(5 - x)}^{2}$
${(P N)}^{2} = 16 - {(5 - x)}^{2} ... . . (i i)$
From Eqs. (i) and (ii),
$9 - x^{2} = 16 - {(5 - x)}^{2}$
$\Rightarrow 7 + x^{2} - (25 + x^{2} - 10 x) = 0$
$\Rightarrow 10 x = 18$
$∴ x = 18$
Again, in right angled $Δ O P N$ ,
$O P^{2} = {(O N)}^{2} + {(N P)}^{2}$ [by Pythagoras theorem]
$\Rightarrow 3^{2} = {(1.8)}^{2} + {(N P)}^{2}$
$\Rightarrow {(N P)}^{2} = 9 - 3.24 = 5.76$
$∴ (N P) = 2.4$
:. Length of common chord, $P Q = 2 P N = 2 \times 2.4 = 4.8 c m$

Updated on:21/07/2023