Let's denotes the semi-perimeter of a ΔABC in which BC=a, CA=b and AB=c. If a circle touches the sides BC, CA, AB, at D, E, F, respectively. Prove that BD=s-b.
A circle is inscribed in the ΔABC, which touches the BC, CA and AB.
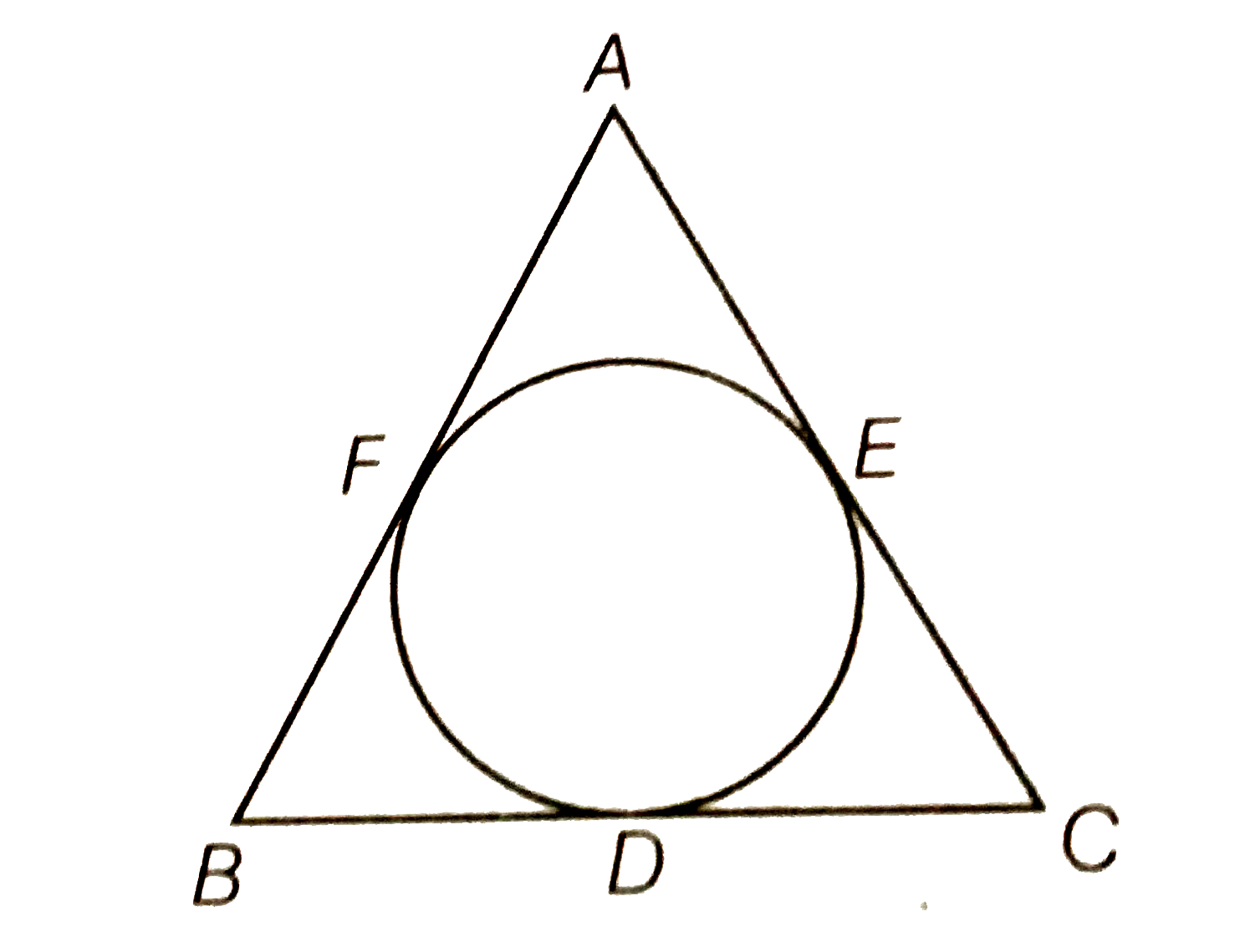
Given, BC=a, CA=b and AB=c
By using the property, tangents are drawn from an external point to the circle are equal in length.
∴BD=BF=x [say]
DC=CE=y [say] and AE=AF=z [say]
Now, BC+CA+AB=a+b+c ⇒(BO+DC)+(CE+EA)+(AF+FB)=a+b+c
⇒(x+y)+(y+z)+(z+x)=a+b+c
⇒2(x+y+z)=2s
[∴2s=a+b+c=perimeter of ΔABC]
⇒s=x+y+z
⇒x=s−(y+z)
⇒BD=s−b [∵b=AE+EC=z+y]
Hence proved.
Topper's Solved these Questions
Similar Questions
Let's denote the semi-perimeter of a triangle ABC in which BC = a, CA = 5, AB = c. If a circle touches the side BC, CA, AB at D, E, F respectively, prove that BD = S-b.
View SolutionThe incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.

View Solution
Knowledge Check
The in circle of ΔABC touches the sides BC, CA and AB at D, E and F respectively. Then AF + BD + CE is equal to :
A12 (Perimeter of Δ ABC)B13 (Perimeter of Δ ABC)C14 (Perimeter of Δ ABC)DPerimeter of Δ ABCLet ∠A=23∘,∠B=75∘and∠C=82∘ be the angles of ΔABC.
The incircle of ΔABC touches the sides BC, CA, AB at points D, E, F respectively. Let r',r′1 respectively be the inradius, exradius opposite to vertex D of ΔDEF and r be inradius of ΔABC, then
Q. r'r=AsinA2+sinB2+sinC2−1B1−sinA2+sinB2+sinC2CcosA2+cosB2+cosC2−1D1−cosA2+cosB2+cosC2Let ∠A=23∘,∠B=75∘and∠C=82∘ be the angles of ΔABC.
The incircle of ΔABC touches the sides BC, CA, AB at points D, E, F respectively. Let r',r′1 respectively be the inradius, exradius opposite to vertex D of ΔDEF and r be inradius of ΔABC, then
Q. r′1r=AsinA2+sinB2+sinC2−1B1−sinA2+sinB2+sinC2CcosA2+cosB2+cosC2−1D1−cosA2+cosB2+cosC2
The incircle of an isosceles triangle ABC, with AB=AC, touches the sides AB, BC, CA at D,E and F respectively. Prove that E bisects BC.
View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
View SolutionLet ∠A=23∘,∠B=75∘and∠C=82∘ be the angles of ΔABC.
The incircle of ΔABC touches the sides BC, CA, AB at points D, E, F respectively. Let r',r′1 respectively be the inradius, exradius opposite to vertex D of ΔDEF and r be inradius of ΔABC, then
Q. r′1r=
View SolutionLet ∠A=23∘,∠B=75∘and∠C=82∘ be the angles of ΔABC.
The incircle of ΔABC touches the sides BC, CA, AB at points D, E, F respectively. Let r',r′1 respectively be the inradius, exradius opposite to vertex D of ΔDEF and r be inradius of ΔABC, then
Q. r'r=
View SolutionIncircle of ΔABC touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
∠DEF is equal to
View Solution
