Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
To prove ∠1=∠2, let PQ be a chord of the circle. Tangents are drawn at the points R and Q.
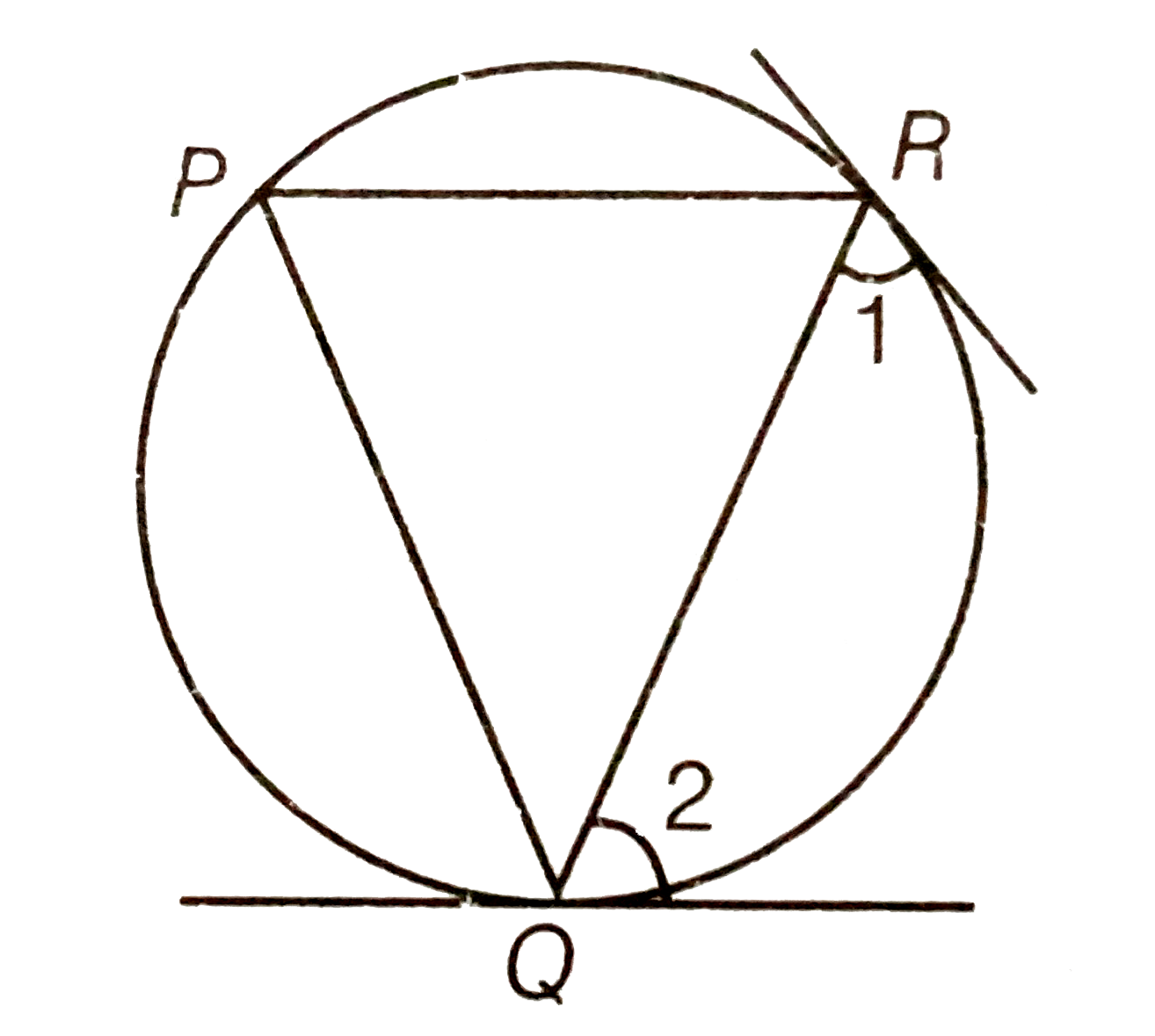
Let P be another point on the circle, then join PQ and PR.
Since, at point Q there is a tangent.
∴∠2=∠P [angles in alternate segments are equal]
Since, at point R, there is a tangent.
∴∠1=∠P
[angles in alternate segments are equal]
∠1=∠2=∠P Hence proved.
Topper's Solved these Questions
Similar Questions
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that the tangents drawn at the ends of the diameter of a circle are parallel.
View Solutionprove that the line joining the mid-point of two equal chords of a circle subtends equal angles with the chord.
View SolutionProve that the tangents at the extremities of any chord make equal angles with the chord.
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionProve that tangent drawn at the mid point of the are of a circle is pallelar to the chord joing the ends of point of the are
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
View SolutionProve that the lengths of tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that equal chords of a circle subtend equal angles at the centre.
View Solution
