In figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.

Given Common tangents AB and CD to two circles interescting at E.
To prove A
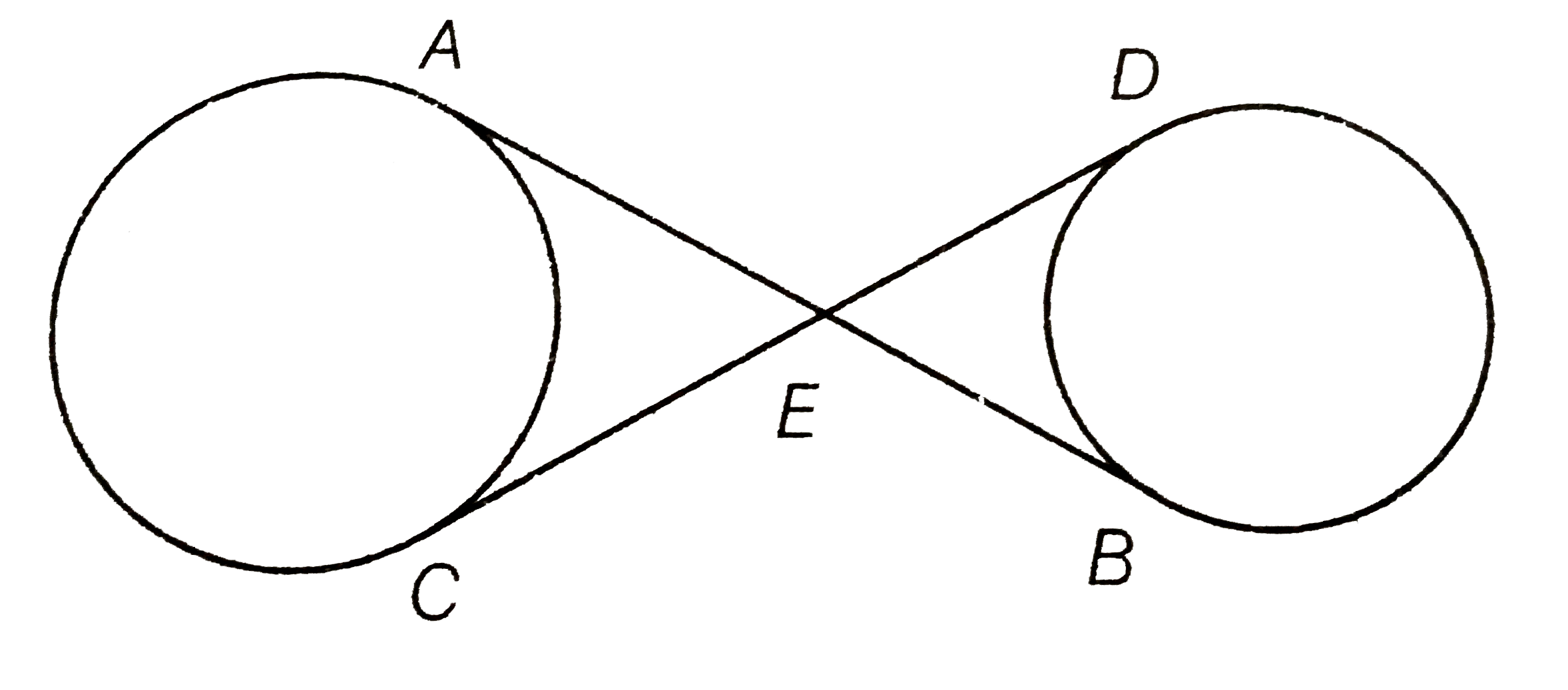
Proof EB=ED…..(i)
[the lengths of tangents drawn from an internal point to a circle are equal]
EB=ED......(ii)
On adding Eqs. (i) and (ii), we get
EA+EB=EC+ED
⇒AB=CD Hence proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
CD is direct common tangent to two circles intersecting each other at A and B. The ∠CAD+∠CBD is equal to
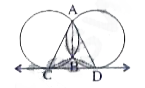 A120∘B90∘C360∘D180∘
A120∘B90∘C360∘D180∘
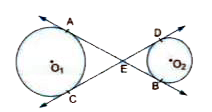
In Fig common tangents AB and CD to two circles with centres O1andO2 intersect at E. Prove that AB = CD.
View SolutionIn figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.

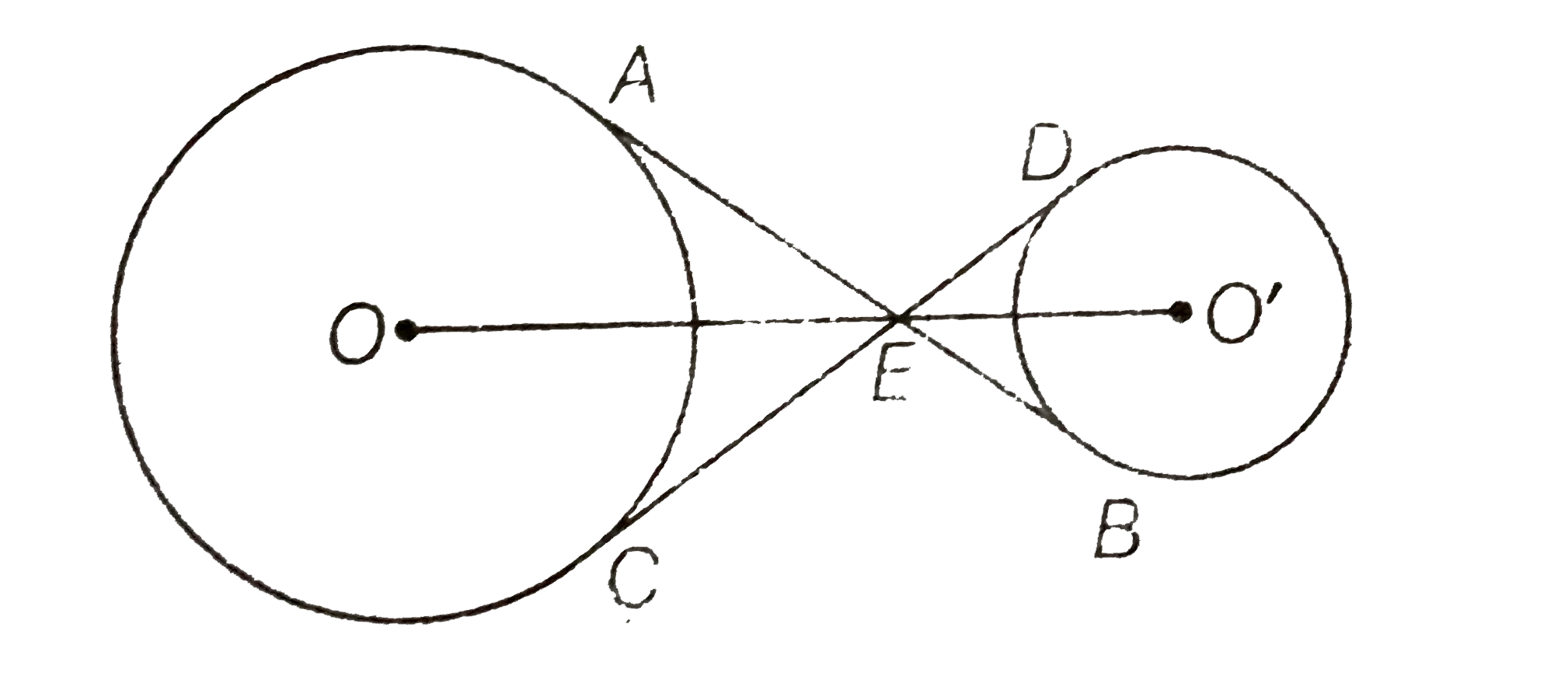
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
View SolutionIn figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB=CD

View SolutionCommon tangents AB and CD to two circles intersect at P, as shown in the figure. If radius OA = 5 cm, radius O'B=3 cm and the distance between the centres OO'= 16cm, then find OP
View SolutionThe common tangents AB and CD to two circles with centres O and O' intersect at E between the centres. Prove that the points O, E and O' are collinear.
View SolutionCD is direct common tangent to two circles intersecting each other at A and B. The ∠CAD+∠CBD is equal to

View Solution


