AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tangent at C intersects AB extended at D, then BC=BD.
To solve the problem step by step, we will use the properties of circles, triangles, and angles.
1. Identify the Given Information:
- AB is the diameter of the circle.
- AC is a chord such that ∠BAC = 30°.
- D is the point where the tangent at C intersects the extended line of AB.
2. Draw the Circle and Label Points:
- Draw a circle with center O.
- Mark points A and B on the circle such that AB is the diameter.
- Mark point C on the circle such that AC is a chord.
- Extend line AB to point D where the tangent at point C intersects.
3. Use the Properties of the Circle:
- Since AB is the diameter, by the Inscribed Angle Theorem, ∠ACB = 90° (an angle inscribed in a semicircle is a right angle).
4. Analyze Triangle OAC:
- In triangle OAC, OA = OC (both are radii of the circle).
- Therefore, triangle OAC is isosceles.
- Let ∠OAC = ∠OCA = x.
- We know that ∠BAC = 30°.
- Thus, ∠AOC = ∠OAC + ∠OCA = x + x = 2x.
- Since the sum of angles in triangle OAC is 180°, we have:
30°+2x+90°=180°
2x=180°−120°=60°
x=30°
- Therefore, ∠OAC = ∠OCA = 30°.
5. Determine Other Angles:
- Since ∠ACB = 90°, we can find ∠ABC:
∠ABC=90°−∠OAC=90°−30°=60°.
6. Analyze Triangle OCB:
- In triangle OCB, OC = OB (both are radii).
- Thus, triangle OCB is also isosceles.
- Let ∠OCB = ∠OBC = y.
- We know that ∠ABC = 60°.
- Therefore, ∠OBC + ∠OCB + ∠CBO = 180°:
y+y+60°=180°
2y=120°
y=60°.
- So, ∠OCB = ∠OBC = 60°.
7. Tangent Properties:
- Since CD is a tangent at point C, we know that OC is perpendicular to CD:
∠OCD=90°.
8. Using Linear Pair:
- Since ∠OCD and ∠OCB are supplementary:
∠OCD+∠OCB=180°.
- Thus, ∠OCD = 90° and ∠OCB = 60° implies:
∠OCD+∠OCB=90°+60°=150°.
9. Final Angle Relationships:
- Since ∠OCD = 90° and ∠OCB = 60°, we can conclude that:
∠BCD=∠OCD−∠OCB=90°−60°=30°.
10. Conclusion:
- Since ∠BCD = ∠BDC = 30°, we have:
BC=BD(by the property of equal angles opposite equal sides).
Final Result:
Thus, we have proved that BC = BD.
- AB is the diameter of the circle.
- AC is a chord such that ∠BAC = 30°.
- D is the point where the tangent at C intersects the extended line of AB.
- Draw a circle with center O.
- Mark points A and B on the circle such that AB is the diameter.
- Mark point C on the circle such that AC is a chord.
- Extend line AB to point D where the tangent at point C intersects.
- Since AB is the diameter, by the Inscribed Angle Theorem, ∠ACB = 90° (an angle inscribed in a semicircle is a right angle).
- In triangle OAC, OA = OC (both are radii of the circle).
- Therefore, triangle OAC is isosceles.
- Let ∠OAC = ∠OCA = x.
- We know that ∠BAC = 30°.
- Thus, ∠AOC = ∠OAC + ∠OCA = x + x = 2x.
- Since the sum of angles in triangle OAC is 180°, we have:
30°+2x+90°=180°
2x=180°−120°=60°
x=30°
- Therefore, ∠OAC = ∠OCA = 30°.
- Since ∠ACB = 90°, we can find ∠ABC:
∠ABC=90°−∠OAC=90°−30°=60°.
- In triangle OCB, OC = OB (both are radii).
- Thus, triangle OCB is also isosceles.
- Let ∠OCB = ∠OBC = y.
- We know that ∠ABC = 60°.
- Therefore, ∠OBC + ∠OCB + ∠CBO = 180°:
y+y+60°=180°
2y=120°
y=60°.
- So, ∠OCB = ∠OBC = 60°.
- Since CD is a tangent at point C, we know that OC is perpendicular to CD:
∠OCD=90°.
- Since ∠OCD and ∠OCB are supplementary:
∠OCD+∠OCB=180°.
- Thus, ∠OCD = 90° and ∠OCB = 60° implies:
∠OCD+∠OCB=90°+60°=150°.
- Since ∠OCD = 90° and ∠OCB = 60°, we can conclude that:
∠BCD=∠OCD−∠OCB=90°−60°=30°.
- Since ∠BCD = ∠BDC = 30°, we have:
BC=BD(by the property of equal angles opposite equal sides).
Thus, we have proved that BC = BD.
Topper's Solved these Questions
Similar Questions
AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tangent at C intersects AB extended at D, then BC=BD.
View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View Solution
Knowledge Check
- Question 1 - Select One
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
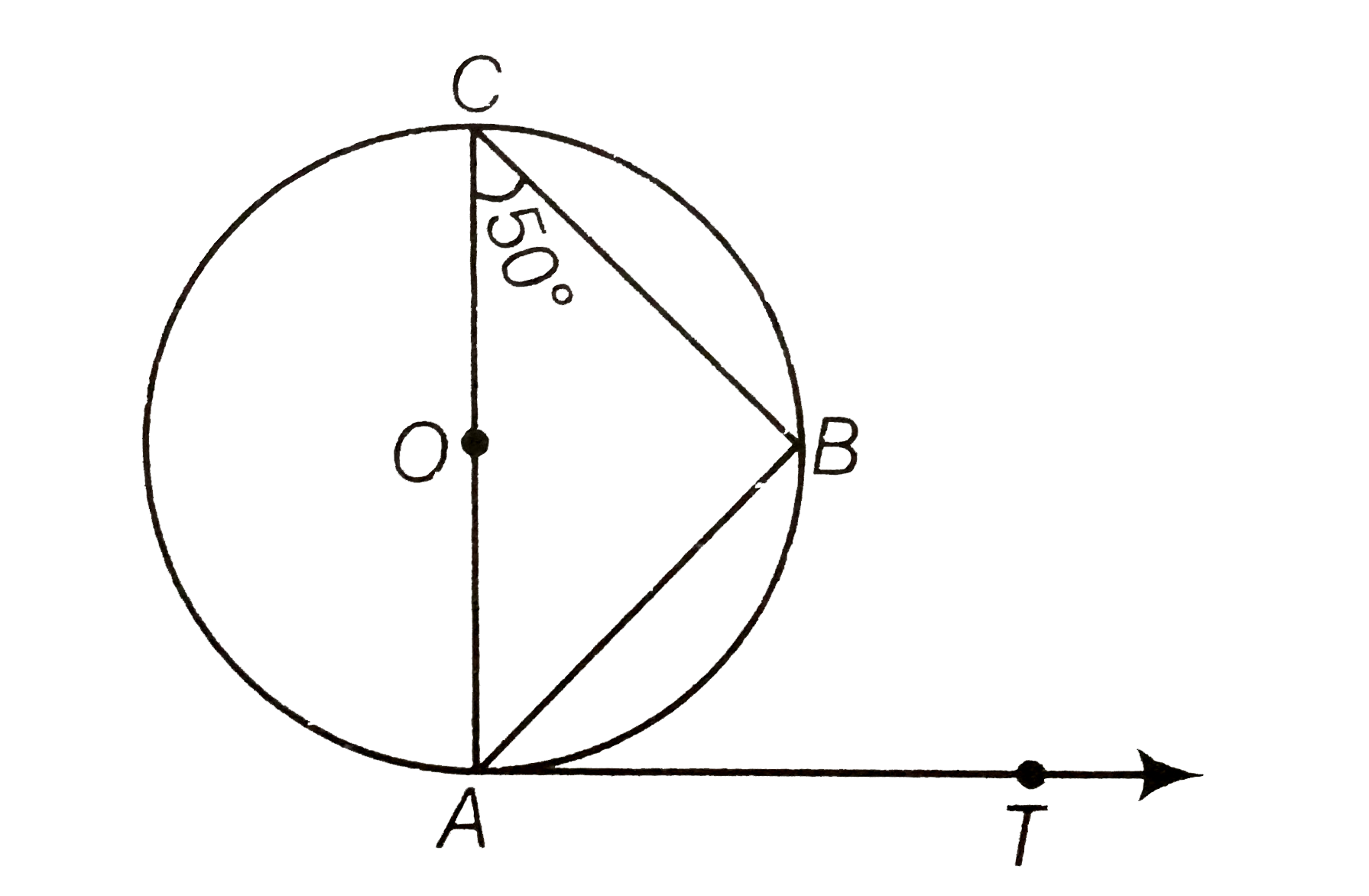 A45∘B60∘C50∘D55∘
A45∘B60∘C50∘D55∘ - Question 2 - Select One
AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
A30∘B60∘C90∘D45∘
AB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD = AB. The tangent at B meets the line AC produced at E then AE is equal to
View SolutionIf AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
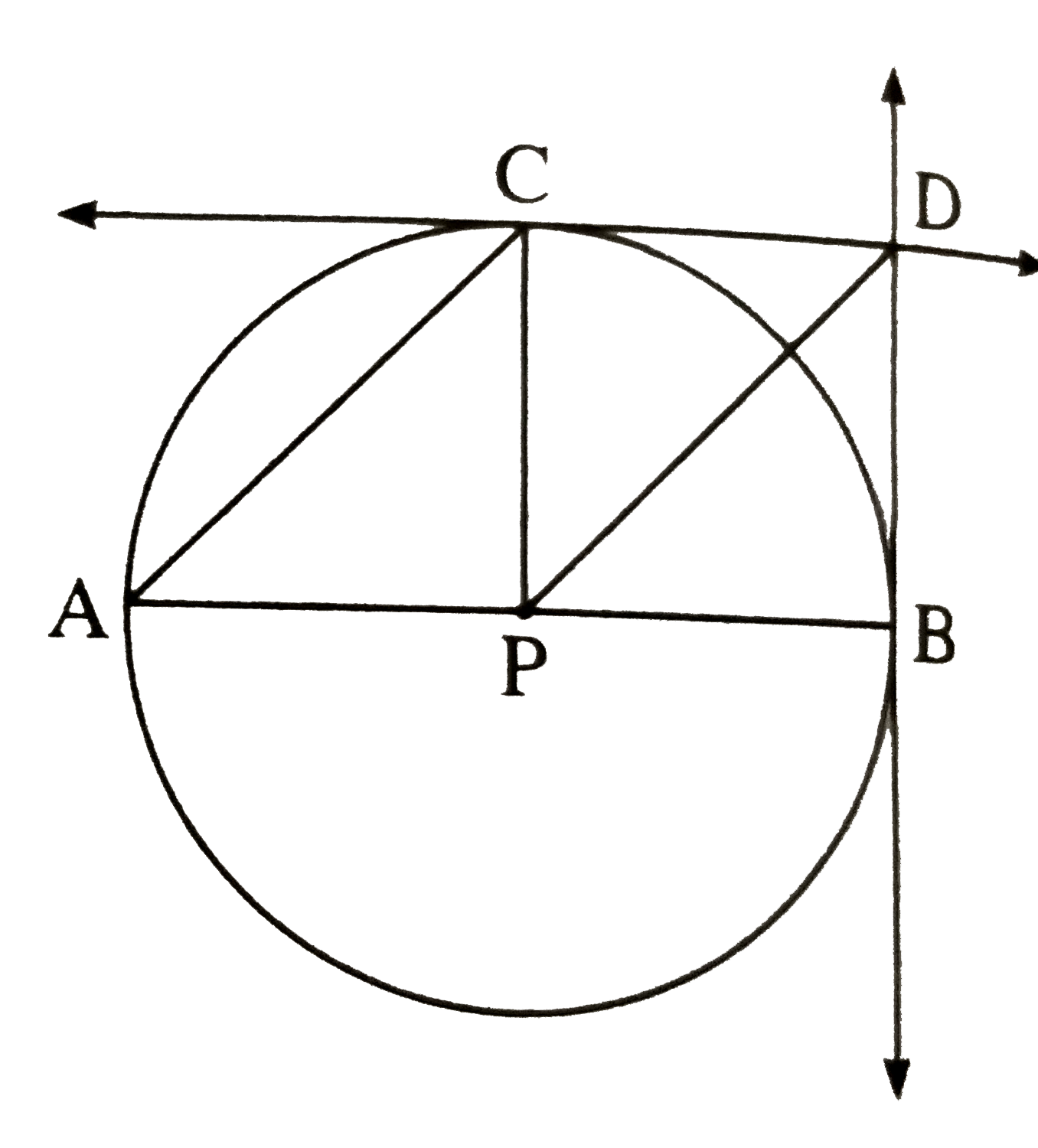 View Solution
View SolutionAB is diameter of a circle with centre 'O'. CD is a chord which is equal to the radius of the circle. AC and BD are extended so that they intersect each other at point P. Then find the value of ∠APB.
View SolutionAB is the diameter of a circle whose centre is O. DC is a chord of that circle. If DC||AB and ∠BAC=20∘ then ∠ADC=?
View Solution

