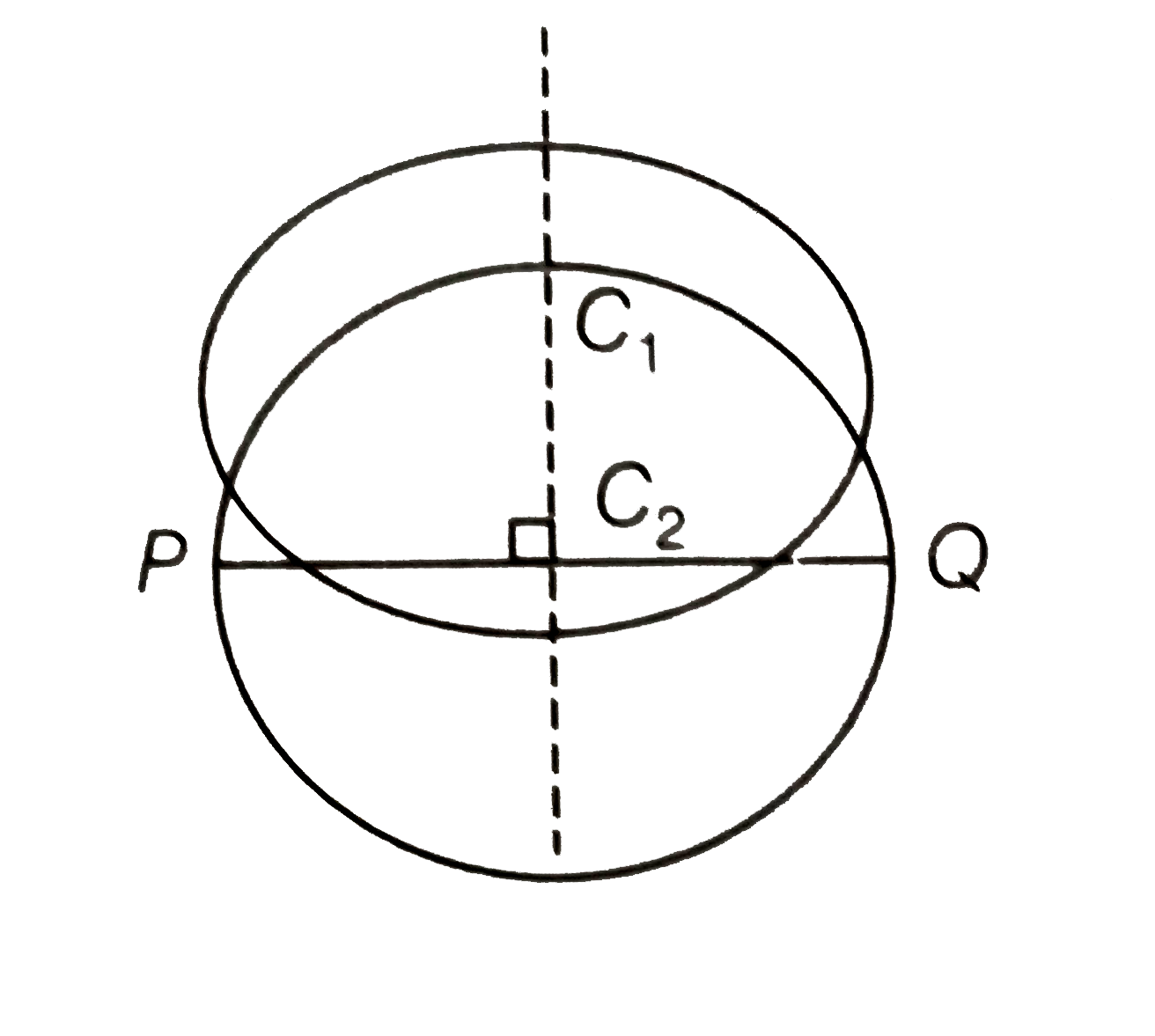
If a number of circles pass through the end points P and Q of a line s

Equation of the plane through the mid-point of the line segment joining the points $P (4, 6, - 10) Q (- 1, 2, 1)$ and perpendicular to PQ is
A $r . (\frac{3}{2} ˆ i + \frac{7}{2} ˆ j - \frac{9}{2} ˆ k) = 45$
B $r . (- ˆ i + 2 ˆ j = ˆ k) = \frac{135}{2}$
C $r . (5 ˆ i + 3 ˆ j - 11 ˆ k) + \frac{135}{2} = 0$
D $r . (5 ˆ i + 3 ˆ j - 11 ˆ k) = \frac{135}{2}$
Consider a circle passing through the origin and the points $(a, b)$ and $(- b, - a) .$ On which line does the centre of the circle lie? What is the sum of the squares of the intercepts cut-off by the circle on the axes?
Ax + y = 0
Bx - y = 0
Cx + y = a + b
Dx - y = $a^{2} - b^{2}$
Equation of the plane through the mid - point of the line segment joining the points P(4,5,-10) and Q (-1,2,1) and perpendicular to PQ is
A $\to r . (\frac{3}{2} ˆ i + \frac{7}{2} ˆ j - \frac{9}{2} ˆ k) = 45$
B $\to r . (- ˆ i + 2 ˆ j - ˆ k) = \frac{135}{2}$
C $\to r . (5 ˆ i + 3 ˆ j - 11 ˆ k) + \frac{135}{2} = 0$
D $\to r . (5 ˆ i + 3 ˆ j - 11 ˆ k) + \frac{135}{2}$

If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.