Two tangents PQ and PR are drawn from an external point to a circle with centre 0. Prove that QORP is cyclic quadrileral.
Given Two tangents PQ and PR are drawn from an external point to a circle with centre O.
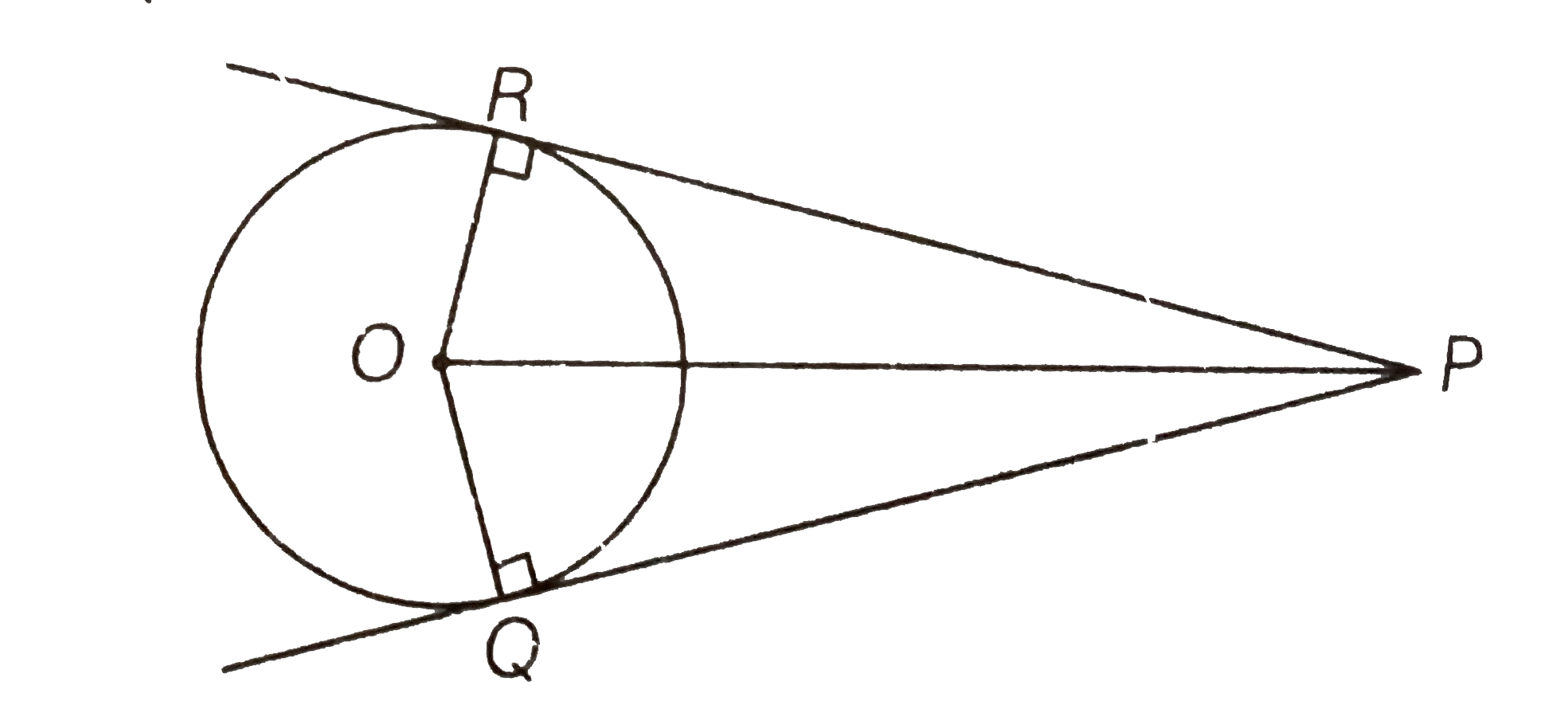
To prove QORP is a cyclic quadrilateral.
proof Since, PR and PQ are tangents.
So, OR⊥PRandOQ⊥PQ
[since, if we drawn a line from centre of a circle to its tangent line. Then the line always perpendicular to the tangent line]
∴∠ORP=∠OQP=90∘
Hence, ∠ORP+∠OQP=180∘
So, QOPR is cyclic quadrilateral.
[If sum of opposite angles is quadrilateral in 180∘ then the quadrilateral is cyclic]
Topper's Solved these Questions
Similar Questions
Two tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
View SolutionTwo tangents AB and AC are drawn from an external point A to a circle with centre O . If they are inclined to each other at an angle of 100∘ then what is the value of ∠BOC.
View Solution
Knowledge Check
In the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPO=30∘. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
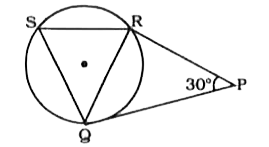 A30∘B50∘C45∘D60∘
A30∘B50∘C45∘D60∘2 equal tangents PA and PB are drawn from an external point P on a circle with centre O. What is the length of each tangent, if P Is 12 cm from the centre and the angle between the tangents is 120∘ ?
A24 cm.B6 cm.C8 cm.DCannot be determinedThe maximum number of tangents drawn from an external point to a circle is :
A0B1C2D4
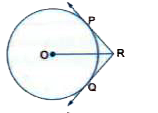
two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR= PR+ RQ
View SolutionIn Fig. two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR = PR + RQ .
View SolutionThe lengths of tangents drawn from an external point to a circle are ________.
View SolutionProve that the lengths of tangents drawn from an external point to a circle are equal.
View SolutionIn the figure , PQ and PR are tangents drawn from and external point P to the circle with centre O. Q and R are the points of contact. If PQ = 5 cm then what is the length of segment PR ? Why ?

View Solution

