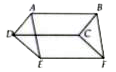
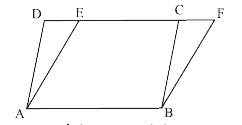
In figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
Video Solution
Text Solution
Given, ABCD and AEFD are two parallelograms.
To prove ar(ΔPEA)=ar(ΔQFD)
Proof In quadrilateral PQDA,
AP∣∣DQ [since, in parallelogram ABCD, AB∣∣CD]
and PQ∣∣AD [since, in parallelogram AEFD, FE∣∣AD]
Then, quadrilateral PQDA is a parallelogram.
Also, parallelogram PQDA and AEFD are on the same base AD and between the same parallels AD and EQ.
∴ ar (parallelogram PQDA) = ar (parallelogram AEFD)
On subtracting ar (quadrilateral APFD) from both sides, we get
ar (parallelogram PQDA)- ar (quadrilateral APFD)
= ar (parallelogram AEFD) - ar (quadrilateral APFD)
⇒ ar(ΔQFD)=ar(ΔPEA) Hence proved.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
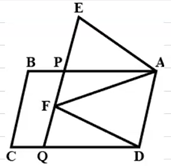
In the given figure, ABCD and AEFD a re two parallelograms.
ar(ΔPEA) =Aar(∣∣gmΔPEA)Bar(ΔPFD)Car(ΔQFD)Dar(∣∣gmΔCQPB)In the given figure, ABCD and AEFD a re two parallelograms.

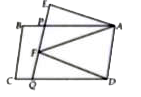
PE =ABPBFQCAPDCQIn the given figure, ABCD and AEFD a re two parallelograms.
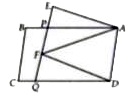
(ar(ΔAPE))/(ar(ΔPFA)) =A(ar(ΔQFD))/(ar(ΔPFD))B(ar(ΔAEF))/(ar(ΔPFD))C(ar(ΔQFD))/(ar(ΔAEF))DNone of these
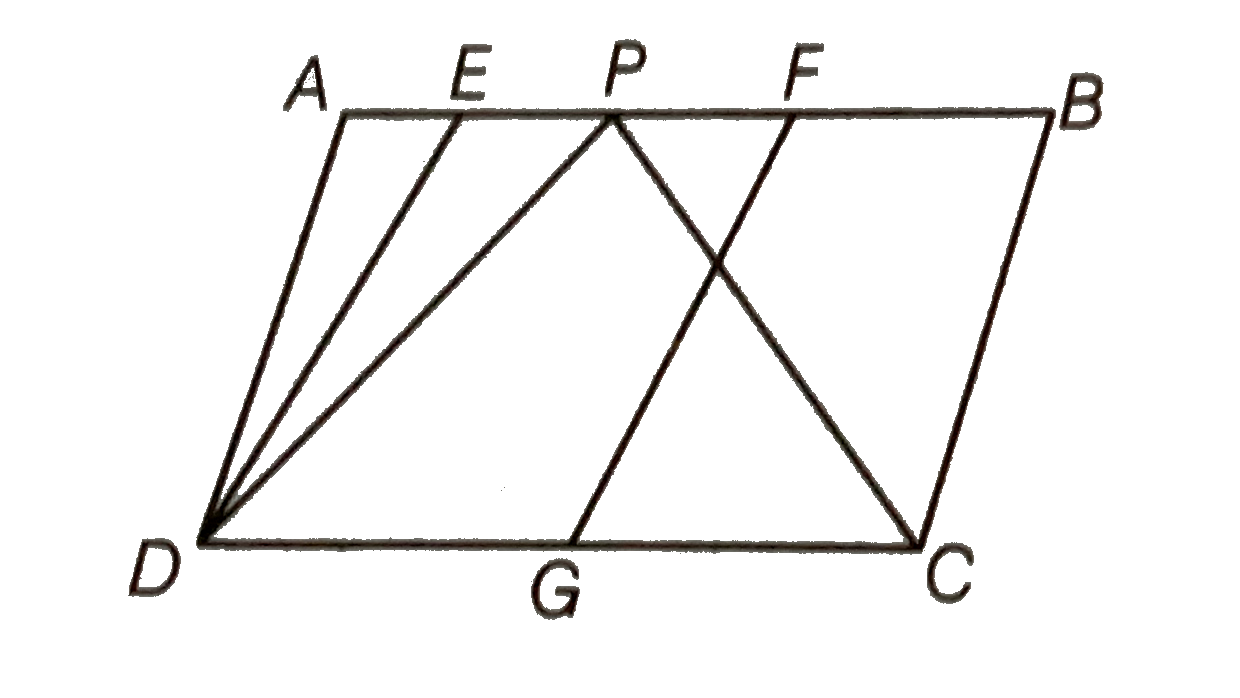
In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE)=ar(BCF).
View SolutionIn the given figure, ABCD and FECG are parallelograms equal in area. If ar(ΔAQE)=12cm2, find ar(∣∣gmFGBQ)
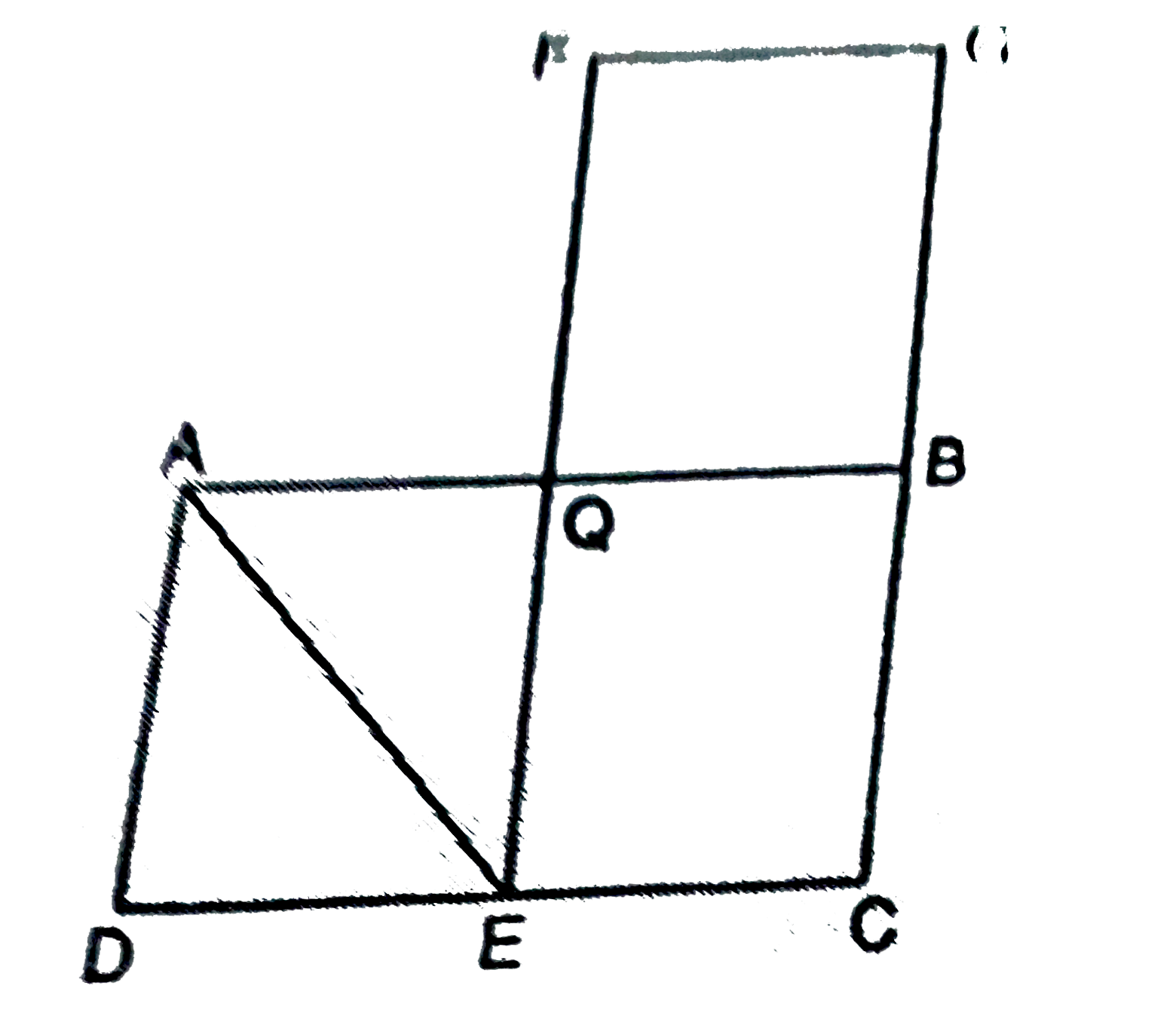
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
View SolutionIn the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
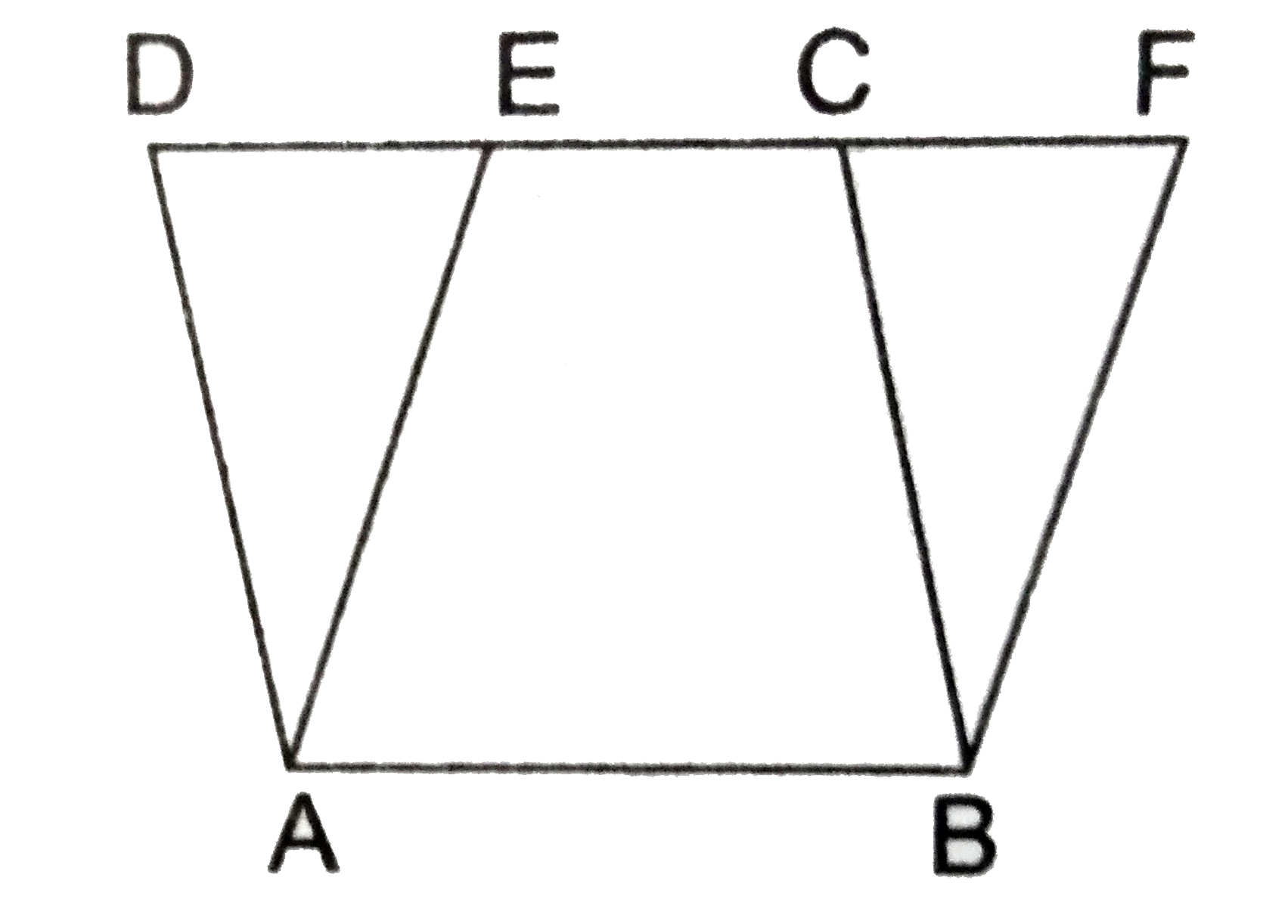
View SolutionIn the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
View Solution