In figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar(ABCDE)=ar(ΔAPQ).
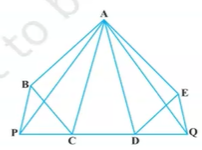
Given ABCDE is a pentagon.
BP∣∣AC and EQ∣∣AD.
To prove ar(ABCDE)=ar(APQ)
Proof We know that, triangles on the same base and between the same parallels are equal in area.
Here, ΔADQ and ΔADE lie on the same base AD and between the same parallels AD and EQ.
So, ar(ΔADQ)=ar(ΔADE) ...(i)
Similarly, ΔACP and ΔACB lie on the same base AC and between the same parallels AC and BP.
So, ar(ΔACP)=ar(ΔACB) ...(ii)
On adding Eqs. (i) and (ii), we get
ar(ΔADQ)+ar(ΔACP)=ar(ΔADE)+ar(ΔACB)
On adding ar(ΔACD) both sides, we get
ar(ΔADQ)+ar(ΔACP)+ar(ΔACD)=ar(ΔADE)+ar(ΔACB)+ar(ΔACD)
⇒ ar(ΔAPQ)=ar(ABCDE) Hence proved.
Topper's Solved these Questions
Similar Questions
The given figure shows a pentagon ABCDE .drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F. Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
View SolutionThe given figure shows a pentagon ABCDE.EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F. Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.

View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that

ar(ΔAEDF) = ar(ΔABCDE)
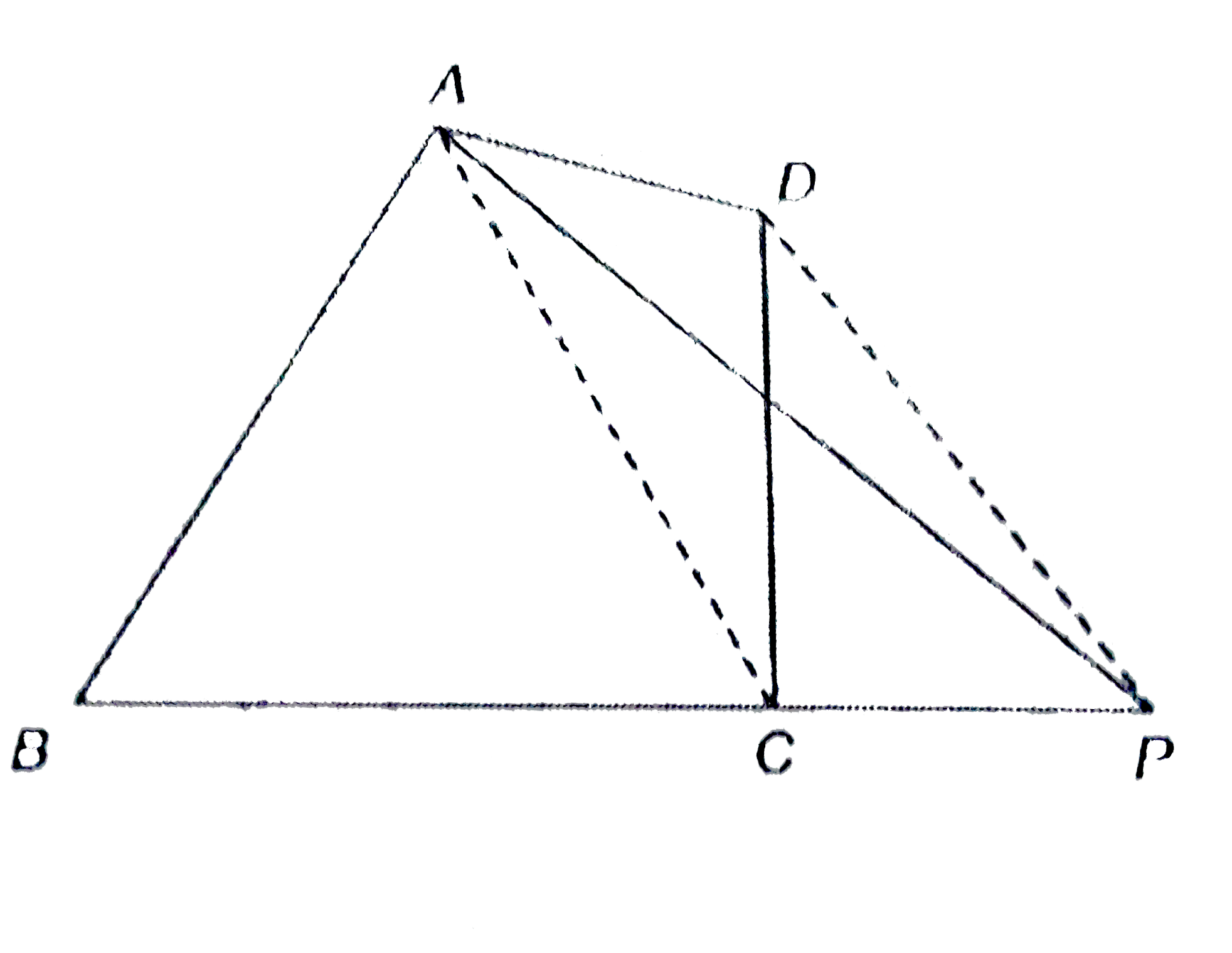
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
area of ΔABP= area of □ABCD
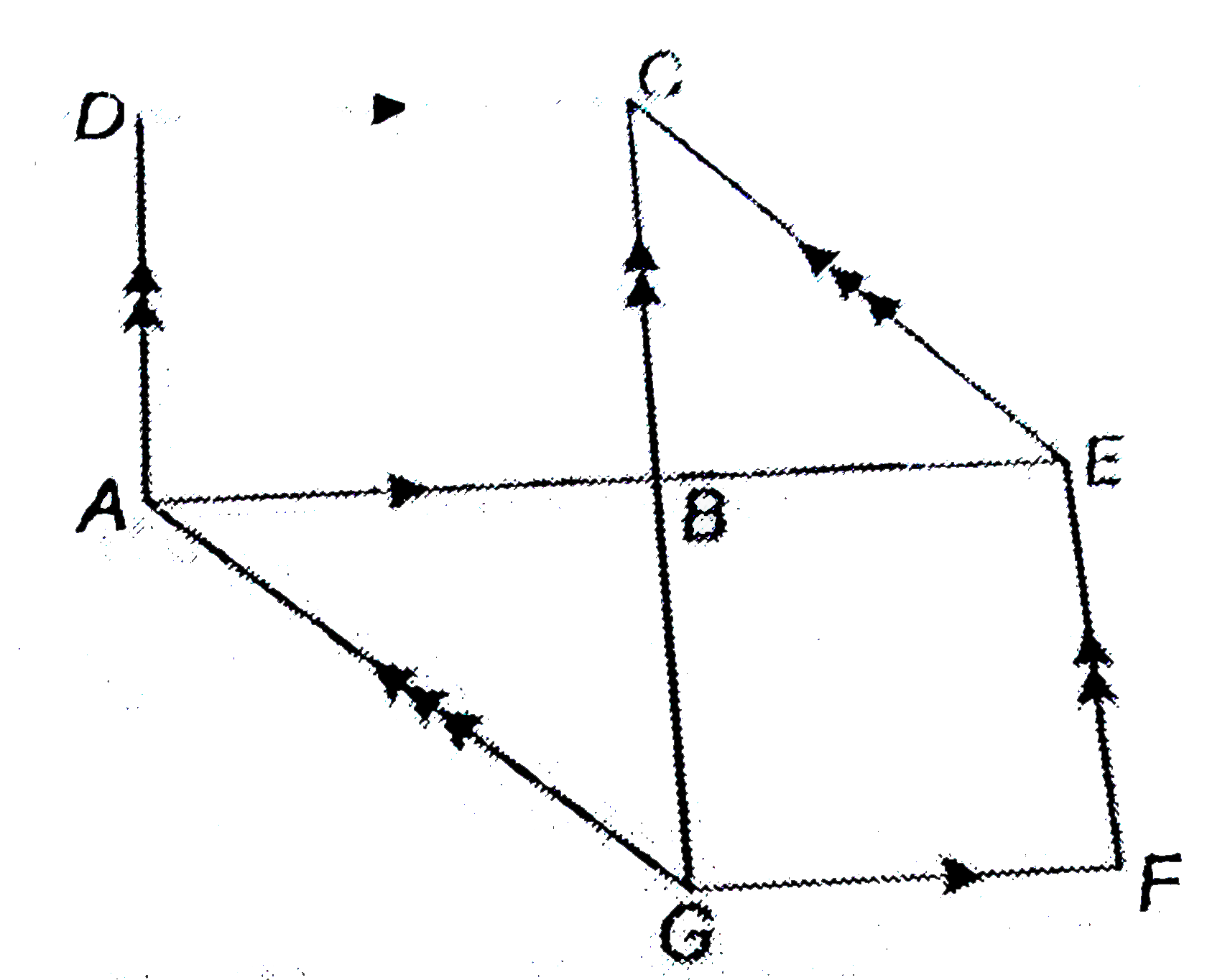
View SolutionThe side AB of a parallelogram ABCD is produced to any point E. A line through A and parallel to CE meets CB produced at G and then parallelogram EBGF is completed (see the figure). Prove that
area of ||gmABCD= area of ||gmBEFG.
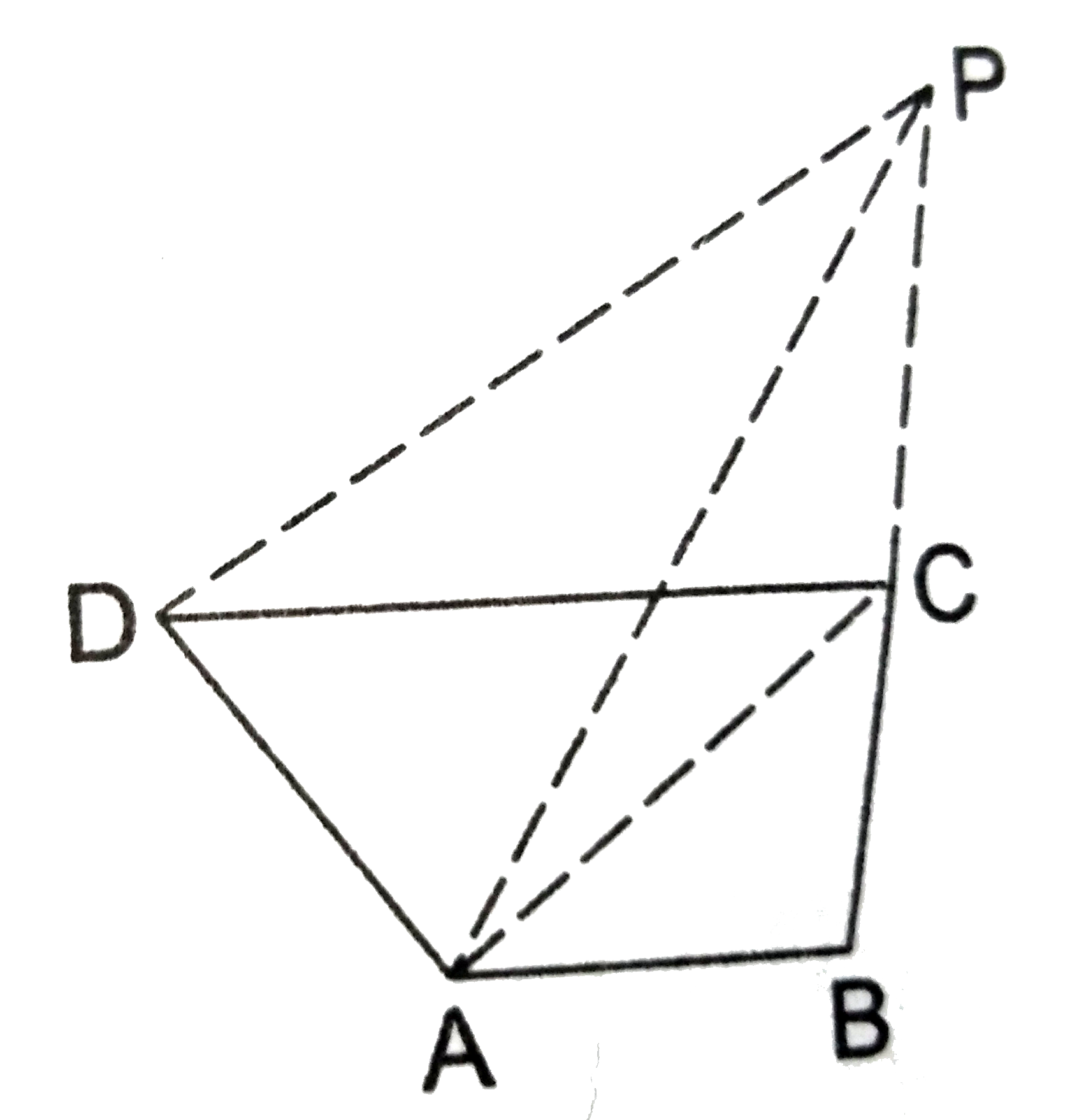
View SolutionIn the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that ar(△ABP)=ar(qaud. ABCD).
View SolutionP is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQ
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(∣∣gmABCD)=ar(∣∣gmPBQR)
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View Solution
