If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram, so formed will be half of the area of the given quadrilateral (figure).

Video Solution

Text Solution

Verified by Experts

Given Let ABCD is a quadrilateral and P, F, R and S are the mid-points of the sides BC, CD, AD and AB respectively and PFRS is a parallelogram.

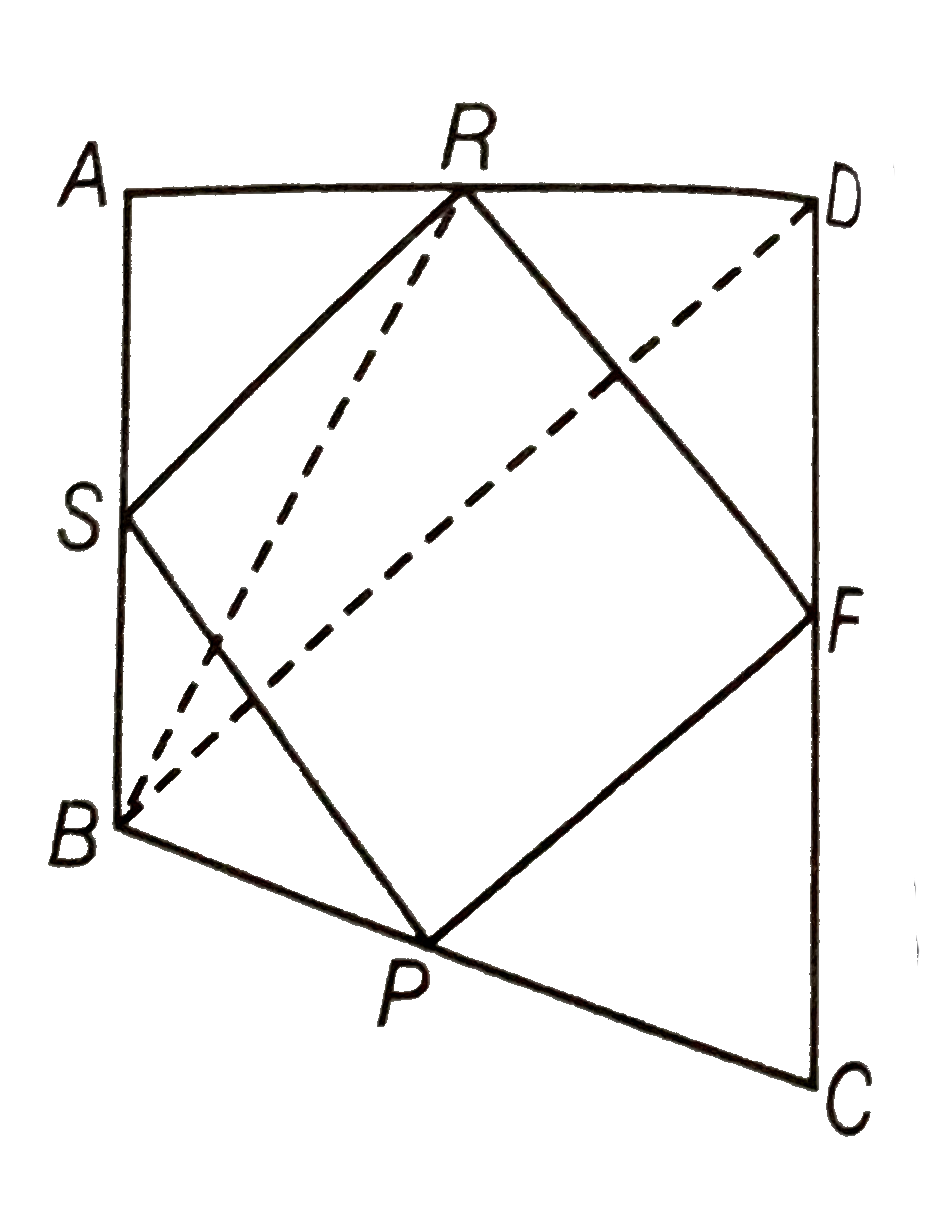
To prove ar (parallelogram PFRS) = $\frac{1}{2} a r (quadrilateral A B C D)$
Construction Join BD and BR.
Proof Median BR divides $Δ B D A$ into two triangles of equal area.
$∴$ $a r (Δ B R A) = \frac{1}{2} a r (Δ B D A)$ ...(i)
Similarly, Median RS divides $Δ B R A$ into two triangles of equal area.
$∴$ $a r (Δ A S R) = \frac{1}{2} a r (Δ B R A)$ ...(ii)
From Eqs. (i) and (ii),
$a r (Δ A S R) = \frac{1}{4} a r (Δ B D A)$ ...(iii)
Similarly, $a r (Δ C F P) = \frac{1}{4} a r (Δ B C D)$ ...(iv)
On adding Eqs. (iii) and (iv), we get
$a r (Δ A S R) + a r (Δ C F P) = \frac{1}{4} a r (Δ B D A)$ [ $a r (Δ B D A) + a r (Δ B C D)$ ]
$\Rightarrow$ $a r (Δ A S R) + a r (Δ C F P) = \frac{1}{4} a r (quadrilateral B C D A)$ ...(v)
Similarly, $a r (Δ D R F) + a r (Δ B S P) = \frac{1}{4} a r (quadrilateral B C D A)$ ...(vi)
On adding Eqs. (v) and (vi), we get
$a r (Δ A S R) + a r (Δ C F P) + a r (Δ D R F) + a r (Δ B S P)$
$= \frac{1}{2} a r (quadrilateral B C D A)$ ...(vii)
But $a r (Δ A S R) + a r (Δ C F P) + a r (Δ D R F) + a r (Δ B S P) + a r (parallelogram P F R S)$
$= a r (quadrilateral B C D A)$ ...(viii)
On subtracting Eq. (vii) from Eq. (viii), we get
$a r (parallelogram P F R S) = \frac{1}{2} a r (quadrilateral B C D A)$ Hence proved.

Updated on:21/07/2023

In the adjoining figure, the area of quadrilateral ABCD is

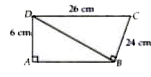A148 $c m^{2}$
B144 $c m^{2}$
C120 $c m^{2}$
D122 $c m^{2}$
The figure formed by joining the mid-points of the sides of a quadrilateral taken in order is
Aparallelogram
Brectange
Csquare
Dnone
The figure formed by joining the mid-points of the sides of a quadrilateral ABCD taken in order is a square only, if
AABCD is a rhombus.
Bdiagonals of ABCD are equal.
Cdiagonals of ABCD are equal and perpendicular.
Ddiagonals of ABCD are perpendicular.