In trapezium ABCD, AB∣∣DC and L is the mid-point of BC. Through L, a line PQ∣∣AD has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).

Given In trapezium ABCD, AB∣∣DC, DC produced in Q and L is the mid-point of BC.
∴ BL = CL
To prove ar(ABCD)=ar(APQD)
Proof Since, DC produced in Q and AB∣∣DC.
So, DQ∣∣AB
In ΔCLQ and ΔBLP,
CL=BL [since, L is the mid-point of BC]
∠LCQ=∠LBP [alternate interior angles as BC is a transversal]
∠CQL=∠LPB [alternate interior angles as PQ is a transversal]
∴ ΔCLQ≅ΔBLP [by AAS congruence rule]
Then, ar(ΔCLQ)=ar(ΔBLP) ...(i)
[since, congruent triangles have equal area]
Now, ar(ABCD)=ar(APQD)−ar(ΔCQL)+ar(ΔBLP)
=ar(APQD)−ar(ΔBLP)+ar(ΔBLP) [from Eq. (i)]
⇒ ar(ABCD)=ar(APQD) Hence proved.
Topper's Solved these Questions
Similar Questions
P is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQ
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View Solution
Knowledge Check
ABCD is a parallelogram and L is a point on DB . The produced line AL meets BC at M and DC produced at N .
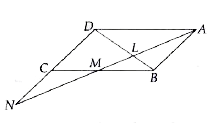
Given that DL =3LB , find ABCN .A3/2B1/2C4/5D1/4
15 O is the point of intersection of the diagonals AC and BD ofa trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. rove that PO=QO ,
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View SolutionIn trapezium ABCD,AB∣∣DCAB=16cm,DC=10cm,AD=CB=5cm then its area is cm2.
View SolutionO is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB||DC. Through O , aline segment PQ is drawn parallel to AB meeting AD in P and BC in Q, prove that PO=QO.
View SolutionIn figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar(ABCDE)=ar(ΔAPQ).
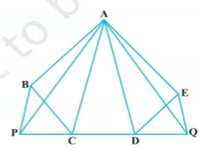
View Solution
