ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
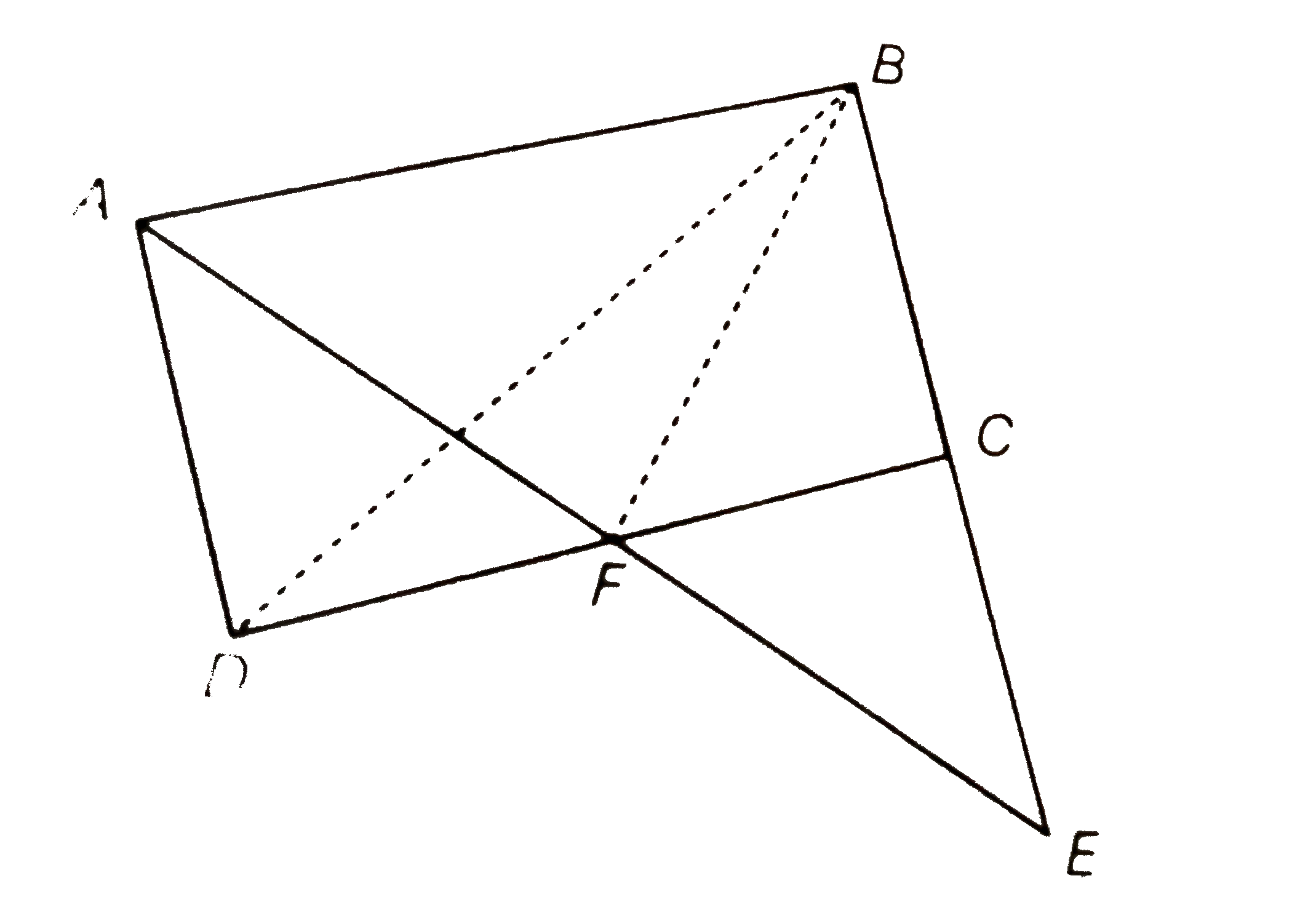
If ar(ΔDFB)=3cm2, then find the area of the parallelogram ABCD.
Video Solution
Text Solution
Given, ABCD is a parallelogram and CE = BC i.e., C is the mid-point of BE.
Also, ar(ΔDFB)=3cm2
Now, ΔADF and ΔDFB are on the same base DF and between parallels CD and AB. Then,
ar(ΔADF)=ar(ΔDFB)=3cm2 ...(i)
In ΔABE, by the converse of mid-point theorem,
EF=AF [since, C is mid-point of BE] ...(ii)
In ΔADF and ΔECF,
∠AFD=∠CFE [Vertically opposite angles]
AF=EF [from Eq. (ii)]
and ∠DAF=∠CEF
[since, BE∣∣AD and AE is transversal, then alternate interior angles are equal]
∴ ΔADF≅ΔECF [by ASA congruence rule]
Then, ar(ΔADF)=ar(ΔCFE) [since, congruent figures have equal area]
∴ ar(ΔCFE)=ar(ΔADF)=3cm2 [from Eq. (i)] ...(iii)
Now, in ΔBFE, C is the mid-point of BE then CF is median of
ΔBFE,
∴ ar(ΔCEF)=ar(ΔBFC) [since, median of a triangle divides it into two triangles of equal area]
⇒ ar(ΔBFC)=3cm2 ...(iv)
Now, ar(ΔBDC)=ar(ΔDFB)+ar(ΔBFC) [from Eqs. (i) and (iv)]
We know that, diagonal of a parallelogram divides it into two congruent triangles of equal areas.
∴ Area of parallelogram ABCD=2×Area of ΔBDC
=2×6=12cm2
Hence, the area of parallelogram ABCD is 12cm2 .
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
A(a) area (ΔBCP) = area (ΔDPQ)B(b) area (ΔBCP)> area (ΔDPQ)C(c) area (ΔBCP)< area (ΔDPQ)D(d) area (ΔBCP) + area (ΔDPQ) = area (ΔBCD)In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1
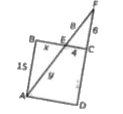
The side AD of parallelogram ABCD is produced to a point E. BE intersects CD at F. Show that ΔABE~ΔCFB.
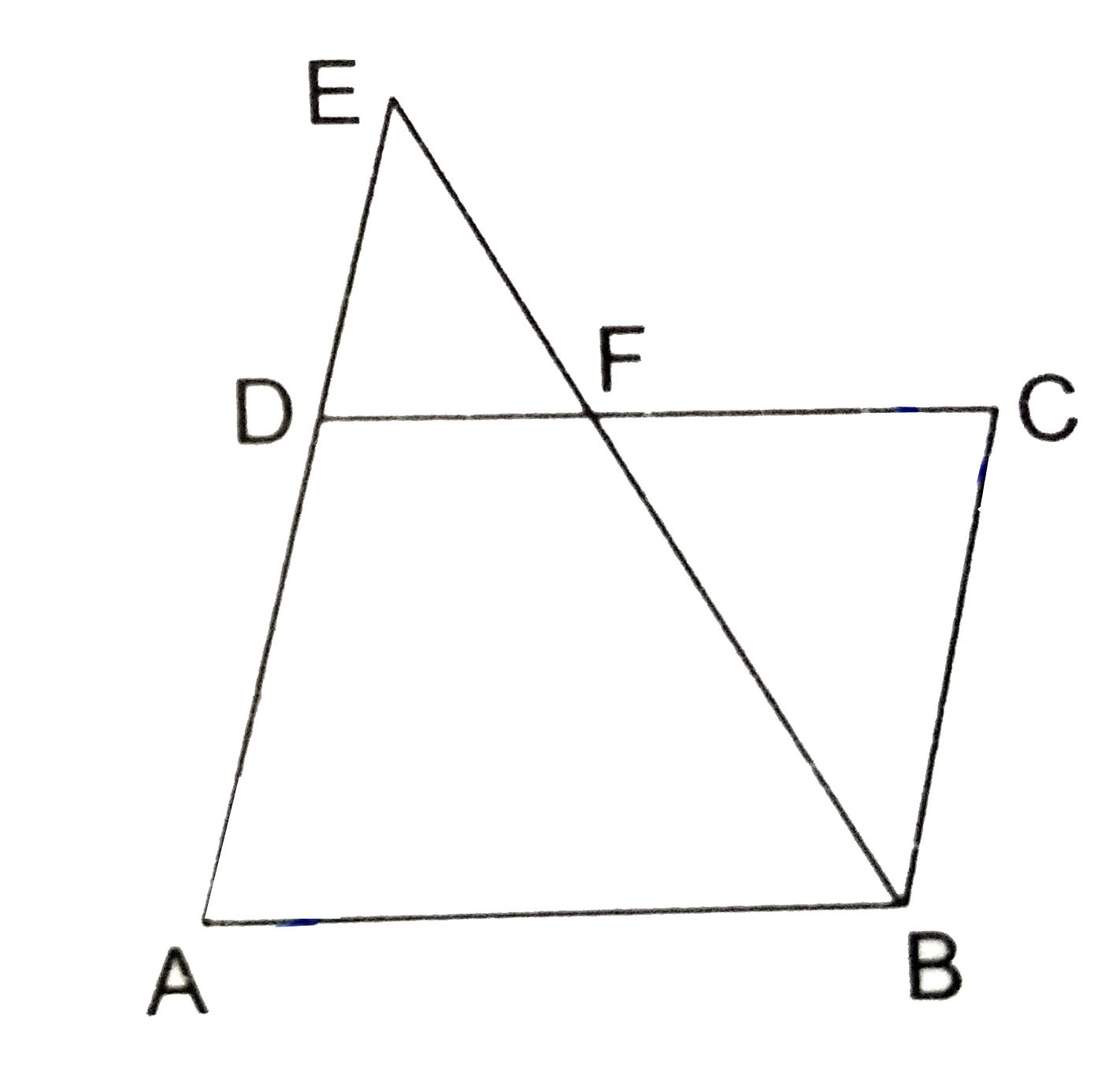
View SolutionIn the given figure, ABCD is a parallelogram in which DC is extended to F such that AF intersects BC at E . Then perimeter of ΔABE=
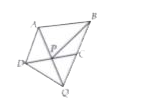
View SolutionIn the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
View SolutionABCD is a parallelogram, P is the mid point of AB. BD and CP intersects at Q such that CQ:QP=3:1. If ar(ΔPBQ)=10cm2, find the area of parallelogram ABCD.
View SolutionABCD is a parallelogram. The circle through A,B and intersects CD produced at E. show that AD =AE.
View SolutionABCD is a parallelogram. The circle through A,BandC intersects CD produced at E, prove that AE=AD.
View Solution
