ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
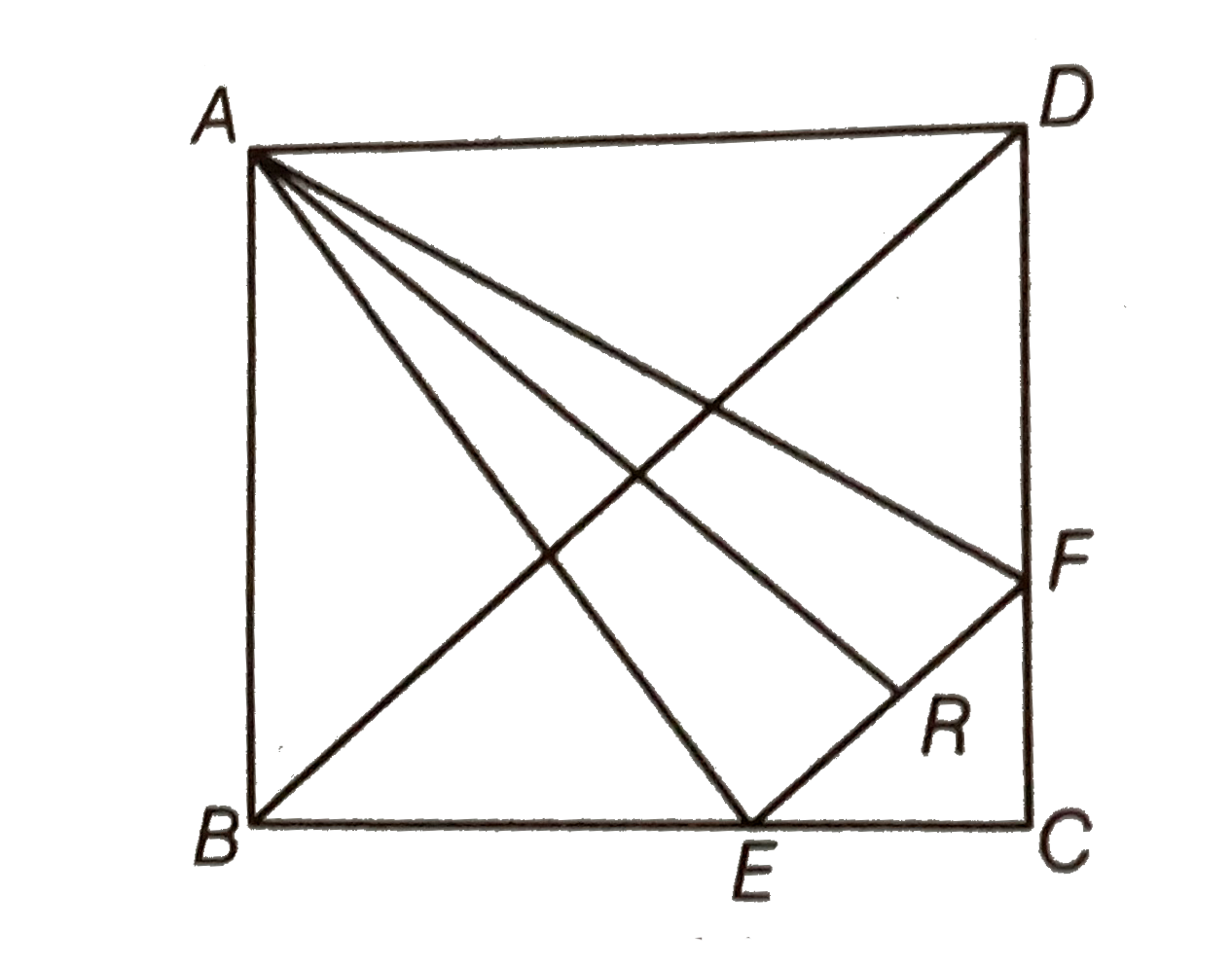
Given In square ABCD, E and F are mid-points of BC and CD respectively. Also, R is the mid-point of EF.
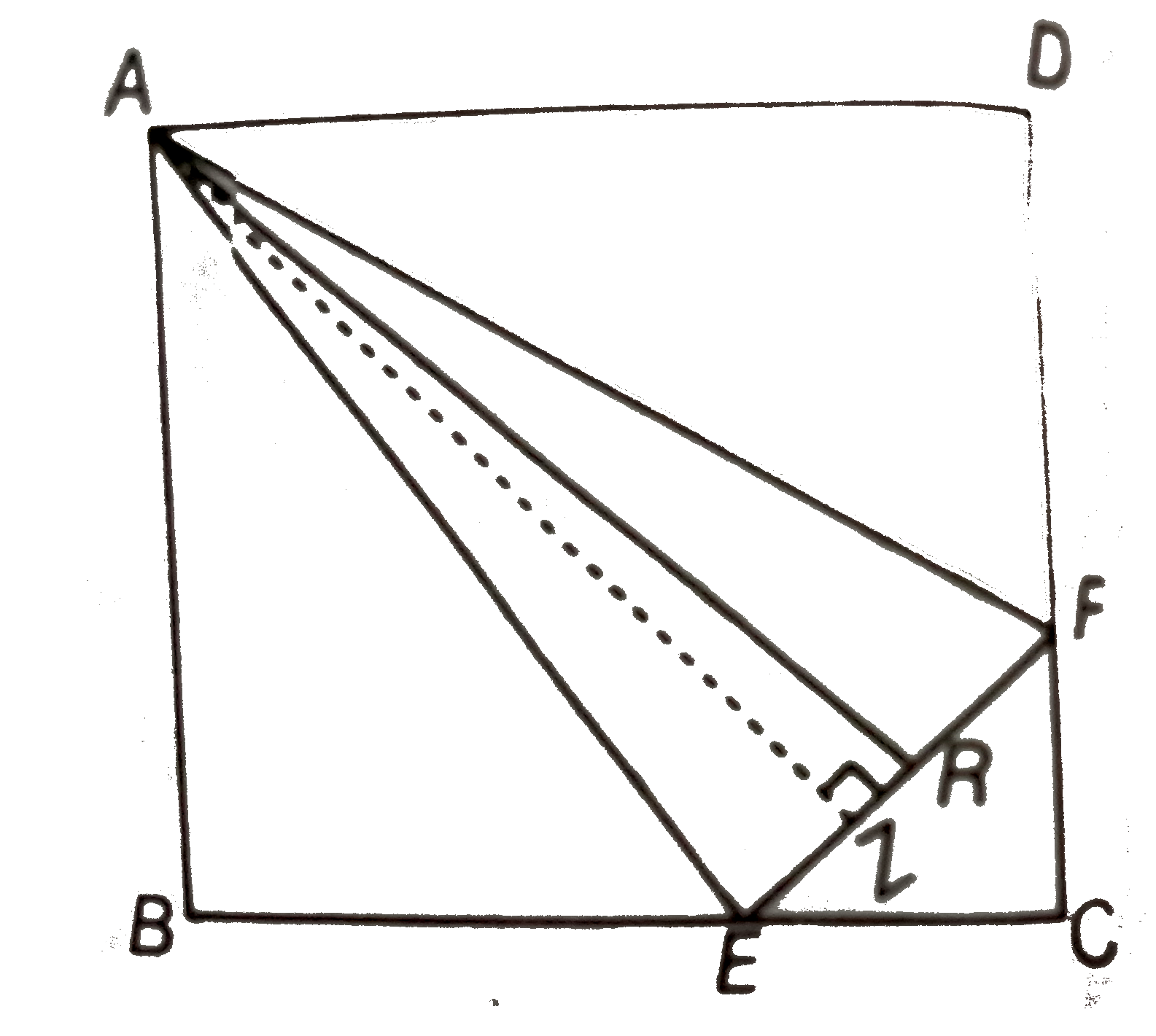
To prove ar(AER)=ar(AFR)
Construction Draw AN⊥EF
Proof ∵ ar(ΔAER)=12×Base×Height
=12×ER×AN
=12×FR×AN [∵ R is the mid-point of EF, so ER = FR]
=ar(ΔAFR) Hence proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
E and F are mid-points of diagonals AC and BD of □ABCD. If G is the mid-point of seg EF, then
A4 ¯¯¯¯¯¯AGB¯0C0D2¯¯¯¯¯¯GC - Question 2 - Select One
ABCD is a parallelogram, E and F are the mid-points of BC and CD. Find the ratio of area of parallelogram ABCD and ΔAEF
A2:1B4:1C8:3D8:1
in figure , M is the mid-point of AB and N is the mid-point of BC (1) if AB=BC , prove that AM=NC
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(BDEF) =12ar(△ABC)View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)View SolutionD is the mid-point of side BC of ΔABC and E is the mid-point of BO. If O is the mid-point of AE, then ar(ΔBOE) = 1/k ar(ΔABC). Then k equals
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn the given figure, ABCD is a rectangle; EandF are the mid-points of the sides BCandCD respectively. What is the ratio of the area of ΔAEF and that of ΔECF?
View Solution

