The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
Given In a parallelogram ABCD, diagonals interect at O and draw a line PQ, which intersects AD and BC.
To prove PQ divides the parallelogram ABCD into two parts of equal area.
i.e., ar(ABQP)=ar(CDPQ)

Proof We know that, diagonals of a parallelogram bisect each other.
∴ OA=OC and OB=OD ...(i)
In ΔAOB and ΔCOD,
OA=OC
OB=OD [from Eq. (i)]
and ∠AOB=∠COD [vertically opposite angles]
∴ ΔAOB≅ΔCOD [by SAS congruence rule]
Then, ar(ΔAOB)=ar(ΔCOD) ...(ii)
[since, cogruent figures have equal area]
Now, in ΔAOP and ΔCOQ
∠PAO=∠OCQ [alternate interior angles]
OA=OC [from Eq. (i)]
and ∠AOP=∠COQ [vertically opposite angles]
∴ ΔAOP≅ΔCOQ [by ASA congruence rule]
∴ ar(ΔAOP)=ar(ΔCOQ) ...(iii)
[since, congruent figures have equal area]
Similarly, ar(ΔPOD)=ar(ΔBOQ) ...(iv)
Now, ar(ABQP)=ar(ΔCOQ)+ar(ΔCOD)+ar(ΔPOD)
=ar(ΔAOP)+ar(ΔAOB)+ar(ΔBOQ) [from Eqs. (ii), (iii) and (iv)]
⇒ ar(ABQP)=ar(CDPQ) Hence proved.
Topper's Solved these Questions
Similar Questions
The diagonals of a parallelogram ABCD intersect at a point O. Through O , a time is drawn to intersect AD at P and BC at Q . Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View Solution
Knowledge Check
AY and BZ are the diagonals of a parallelogram ABYZ, intersecting at O.ar(ΔBYZ) = ?
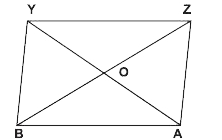 Agreater than ar(ΔABZ)Bis equal to ar(ΔBOA+ΔBOY)Cmore than ar(ΔBOA+ΔBOY)Dless than ar(ΔBOA+ΔBOY)
Agreater than ar(ΔABZ)Bis equal to ar(ΔBOA+ΔBOY)Cmore than ar(ΔBOA+ΔBOY)Dless than ar(ΔBOA+ΔBOY)
The diagonals of a parallelogram ABCD intersect at O.A line through O intersects AB at X and DC at Y. Prove that OX=OY.
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View Solutiondiagonal of a cocyclic parallelogram ABCD is AC and BD intersection at point R. then
View SolutionIn ABC , PQ is a line segment intersecting AB at P and AC at Q such that PQBC and PQ divides ABC into two parts equal in area. Find BPAB .
View SolutionThe diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in x and CD in Y. Show that ar (AXYX)=12(ar||gm ABCD)
View SolutionThe diagonals of a parallelogram ABCD intersect at O. If ∠DBC=30∘ and ∠BDC=60∘, then ∠DAB is
View Solution
