In figure, CD∣∣AE and CY∣∣BA. Prove that ar(ΔCBX)=ar(ΔAXY).

Given In figure, CD∣∣AE
and CY∣∣BA
To prove ar(ΔCBX)=ar(ΔAXY)
Proof We know that, triangles on the same base and between the same parallels are equal in areas.
Here, ΔABY and ΔABC both lie on the same base AB and between the same parallels CY and BA.
∴ ar(ΔABY)=ar(ΔABC)
⇒ ar(ABX)+ar(AXY)=ar(ABX)+ar(CBX)
⇒ ar(AXY)=ar(CBX) [eliminating ar (ABX) from both sides]
Hence proved.
Topper's Solved these Questions
Similar Questions
In the given figure, AP||BQ||CR. Prove that ar(ΔAQC)=ar(ΔPBR)

View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
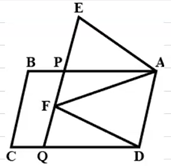
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View SolutionIn Figure, BC||XY,BX||CA and AB∣∣YC Prove that: ar(ABX)=ar(ACY)

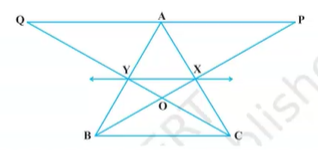
View SolutionIn figure X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar(ΔABP)=ar(ΔACQ).
View SolutionIn ΔABC , if L and M are the points on AB and AC, respectively such that LM∣∣BC. Prove that ar(ΔLOB)=ar(ΔMOC).
View SolutionA point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
View SolutionIn the given figure, if DE||AQ and DF||AR. Prove that EF||QR.

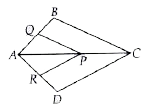
View SolutionIn figure , if PQ||BCandPR||CD . Prove that ARAD=AQAB .
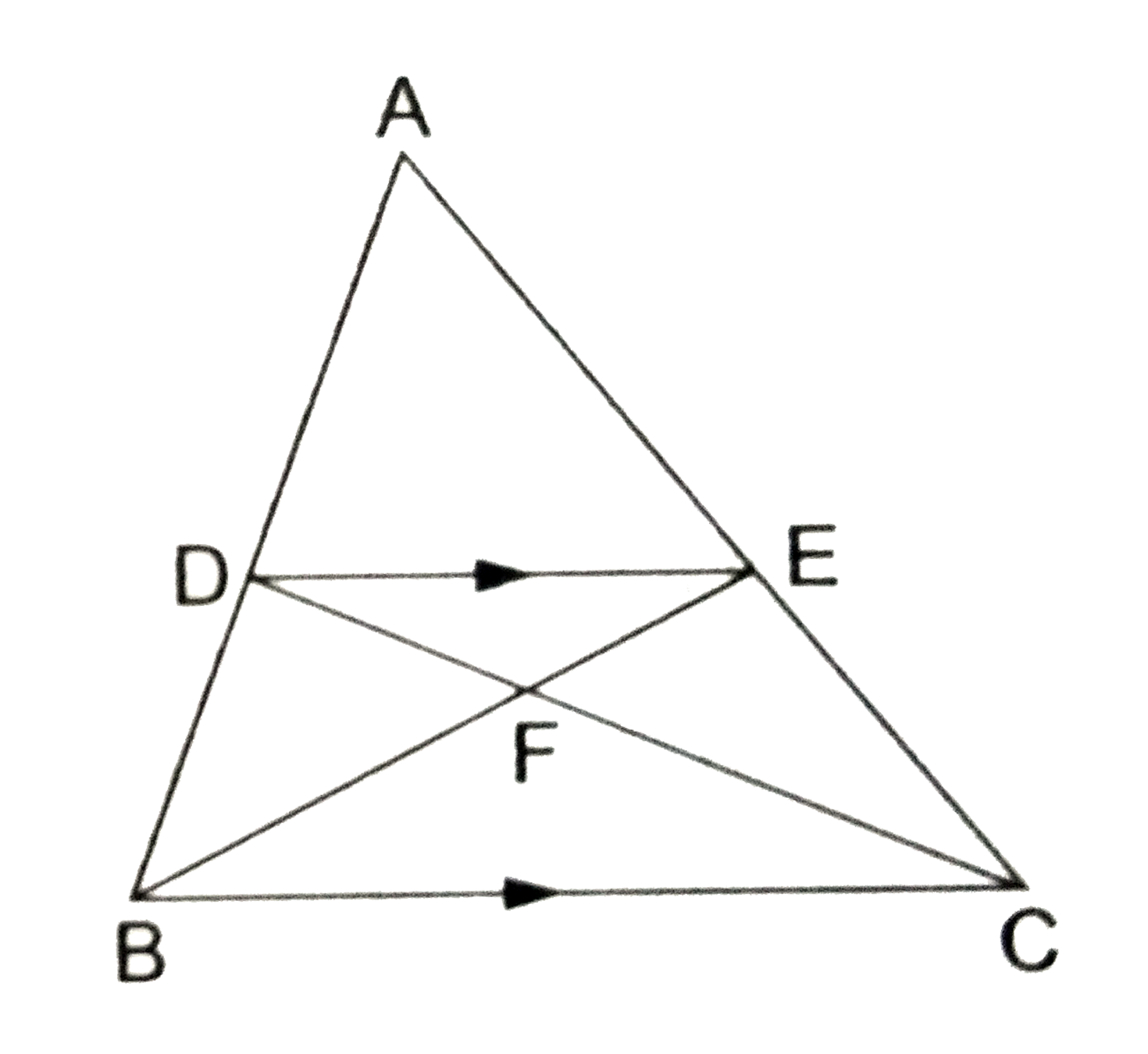
View SolutionIn the given figure DE∣∣BCandAD:DB=5:4
Find the ratio ar(ΔDEF):ar(ΔCFB)
View Solution