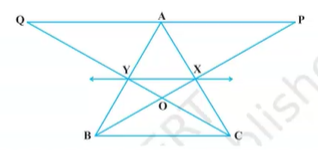
In $Δ A B C$ , if L and M are the points on AB and AC, respectively such that $L M ∣ ∣ B C$ . Prove that $a r (Δ L O B) = a r (Δ M O C)$ .

Video Solution

Text Solution

Verified by Experts

Given In $Δ A B C$ , L and M are points on AB and AC respectively such that $L M ∣ ∣ B C$ .

To prove $a r (Δ L O B) = a r (Δ M O C)$
Proof We know that, triangles on the same base and between the same parallels are equal in area.
Hence, $Δ L B C$ and $Δ M B C$ lie on the same base BC and between the same parallels BC and LM.
So, $a r (Δ L B C) = a r (Δ M B C)$
$\Rightarrow$ $a r (Δ L O B) + a r (Δ B O C) = a r (Δ M O C) + a r (Δ B O C)$
On eliminating D $a r (Δ B O C)$ from both sides, we get
$a r (Δ L O B) = a r (Δ M O C)$ Hence proved.

|

Updated on:21/07/2023

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Topper's Solved these Questions

BOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2videos
CIRCLES

Similar Questions

Knowledge Check

Question 1 - Select One
In $Δ A B C$ , D and E are points on AB and AC respectively such that DE||BC and DE divides the $Δ A B C$ into two parts of equal areas. Then ratio of AD and BD is
A $1 : 1$
B $1 : \sqrt{2} - 1$
C $1 : \sqrt{2}$
D $1 : \sqrt{2} + 1$
Question 2 - Select One
In $Δ A B C$ , D and E are points on AB and AC respectively such that DE is parallel to BC. If AD= 2 cm, BD = 3 cm, then $\frac{a r (Δ A D E)}{a r (Δ A B C)}$ is
A $\frac{4}{9}$
B $\frac{16}{81}$
C $\frac{4}{25}$
D $\frac{2}{5}$
Question 3 - Select One
L and M are the mid points of AB and BC respectively of $Δ A B C$ , right angled at B . $4 L C^{2} =$

A $A B^{2} + 4 B C^{2}$
B $B C^{2} + 4 A B^{2}$
C $A C^{2} + 4 A B^{2}$
DNone of these

NCERT EXEMPLAR-Areas of Parallelograms and Triangles-Areas Of Parallelograms And Triangles

Home
Ask Doubt
Profile