is a parallelogram. and are points on and respectively and prove that and bisect each other.
To prove that lines LM and BD bisect each other in the parallelogram ABCD, given that AL = CM, we can follow these steps:
Step 1: Understand the Given Information
We have a parallelogram ABCD with points L and M on sides AB and DC respectively such that AL = CM.
Step 2: Express AL and CM in Terms of Other Segments
Since L is on AB and M is on DC, we can express:
- AL = AB - BL
- CM = CD - DM
Step 3: Use the Properties of Parallelograms
In parallelogram ABCD, we know that opposite sides are equal:
- AB = CD
Step 4: Set Up the Equation
From the given information AL = CM, we can write:
AB - BL = CD - DM
Since AB = CD, we can substitute:
AB - BL = AB - DM
Step 5: Simplify the Equation
By simplifying the equation, we can cancel out AB from both sides:
- BL = DM
This shows that segments BL and DM are equal.
Step 6: Analyze the Angles
Since AB is parallel to CD and BD is a transversal, we can apply the Alternate Interior Angles Theorem:
- Angle 1 (formed by line LM and line BD) is equal to Angle 2 (formed by line LM and line CD).
- Angle 3 (formed by line BD and line AB) is equal to Angle 4 (formed by line BD and line DC).
Step 7: Use Triangle Congruence
Now, consider triangles OBL and OMD (where O is the intersection point of LM and BD):
- Angle 1 = Angle 2 (from step 6)
- Angle 3 = Angle 4 (from step 6)
- BL = DM (from step 5)
By the Angle-Side-Angle (ASA) criterion, triangles OBL and OMD are congruent.
Step 8: Conclude the Midpoints
From the congruence of triangles OBL and OMD, we can conclude:
- OB = OD
- OL = OM
This means that O is the midpoint of both segments BD and LM.
Step 9: Final Conclusion
Since O is the midpoint of both segments, we conclude that lines LM and BD bisect each other.
We have a parallelogram ABCD with points L and M on sides AB and DC respectively such that AL = CM.
Since L is on AB and M is on DC, we can express:
- AL = AB - BL
- CM = CD - DM
In parallelogram ABCD, we know that opposite sides are equal:
- AB = CD
From the given information AL = CM, we can write:
AB - BL = CD - DM
AB - BL = AB - DM
By simplifying the equation, we can cancel out AB from both sides:
- BL = DM
Since AB is parallel to CD and BD is a transversal, we can apply the Alternate Interior Angles Theorem:
- Angle 1 (formed by line LM and line BD) is equal to Angle 2 (formed by line LM and line CD).
- Angle 3 (formed by line BD and line AB) is equal to Angle 4 (formed by line BD and line DC).
Now, consider triangles OBL and OMD (where O is the intersection point of LM and BD):
- Angle 1 = Angle 2 (from step 6)
- Angle 3 = Angle 4 (from step 6)
- BL = DM (from step 5)
From the congruence of triangles OBL and OMD, we can conclude:
- OB = OD
- OL = OM
Since O is the midpoint of both segments, we conclude that lines LM and BD bisect each other.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM. prove that LM and BD bisect each other.
View SolutionIn a ABC , If LandM are points ABandAC respectively such that LMparallelBC
Prove that: ar(ABM)=ar(ACL)
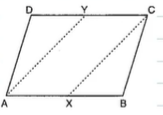
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LCM)=ar(LBM)
View SolutionABCD is a parallelogram X and Y are the mid-points of BC and CD respectively. Prove that ar(AXY)=38ar(∣∣gmABCD)
View SolutionABCD is a parallelogram and line segments AX,CY bisect the angles AandC, respectively. Show that AX∣∣CY
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LBC)=ar(MBC)
View SolutionIn a ABC , If LandM are points on ABandAC respectively such that LMparallel BC
Prove that: ar(LOB)=ar(MOC)
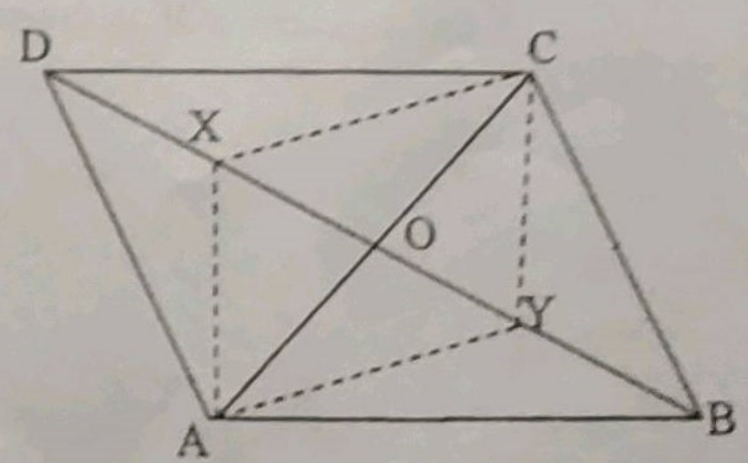
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
View Solution