P is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQ
In ΔARB,P is the mid-point of AB and PD is a parallel to BR.
∴ D will be the mid-point of AR.
i.e. AR=2AD
But ABCD is a parallelogram.
∴AD=BCTherefore,AR=2BC
Which is part (i).
□ABCD is a parallelogram.
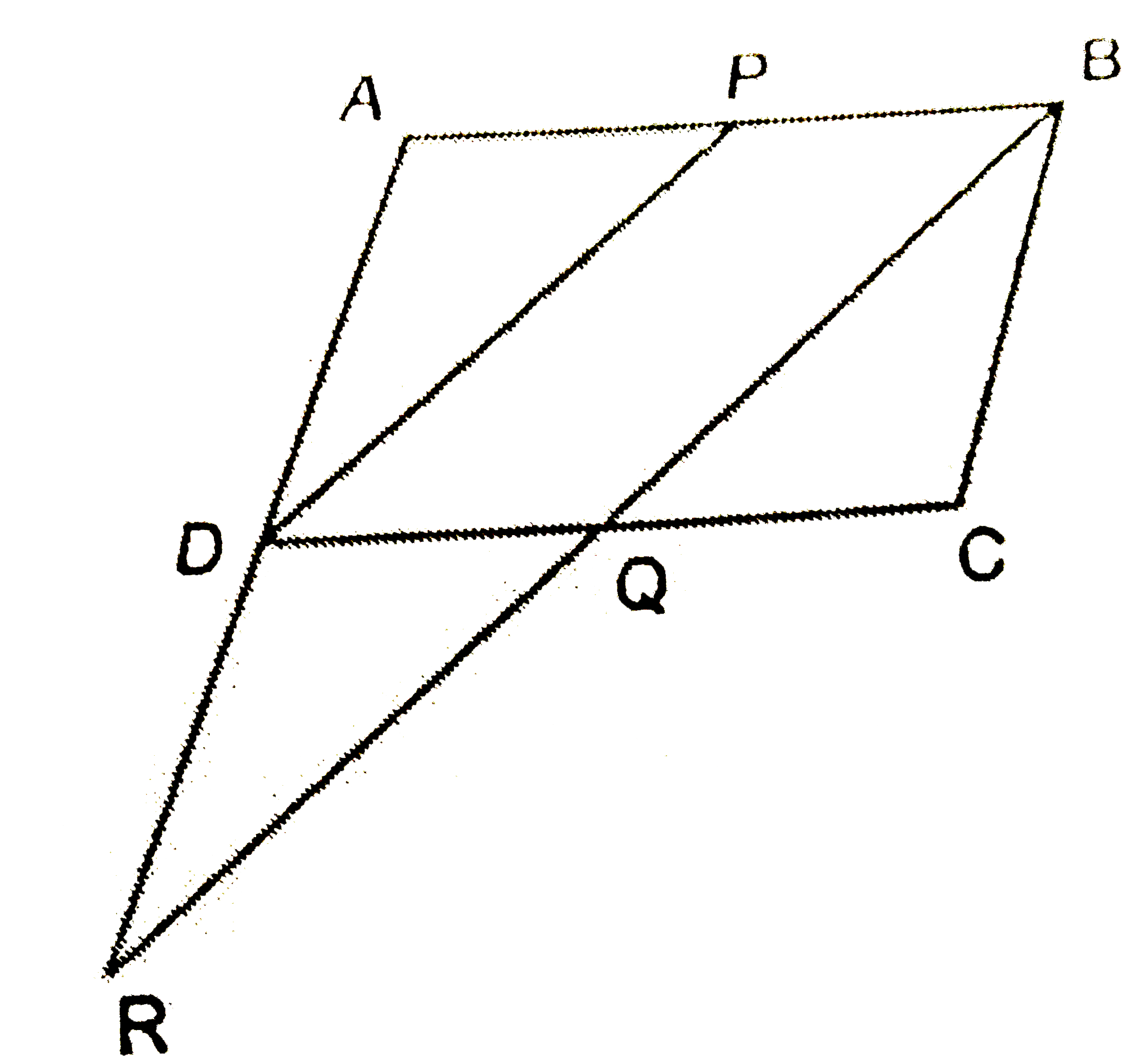
==⇒DC||AB==⇒DQ||AB
In ΔRAB
D is the mid-point of RA.
and DQ||AB
∴ Q is the mid-point of RB.
⇒ BR=2BQ
which is part (ii)
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHANChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHANChapter:STATISTICSExercise:Revision Exercise
Explore 10 Videos
Similar Questions
P is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View Solution
Knowledge Check
E is the mid-point of the side AD of the trapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. then
APoint F trisect BCBPoint F bisect BCCAB=CDDNone
P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
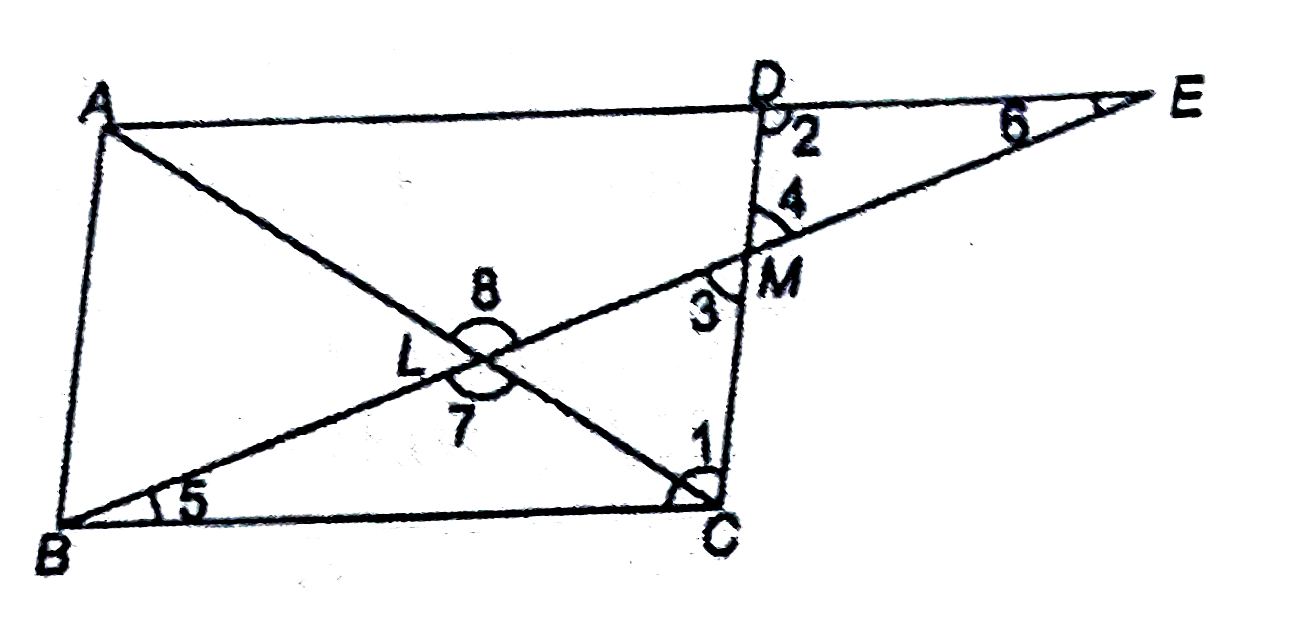
View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn, intersecting AC in L and AD produced in El. Prove that EL= 2BL
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View SolutionP is the mid-point of the side AD of the parallelo- gram ABCD. The line BP meets the diagonal AC in Q and the line CD in R. Then RQ:QB is equal to
View SolutionM is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(i)DMMN=DCBN (ii)DNDM=ANDC

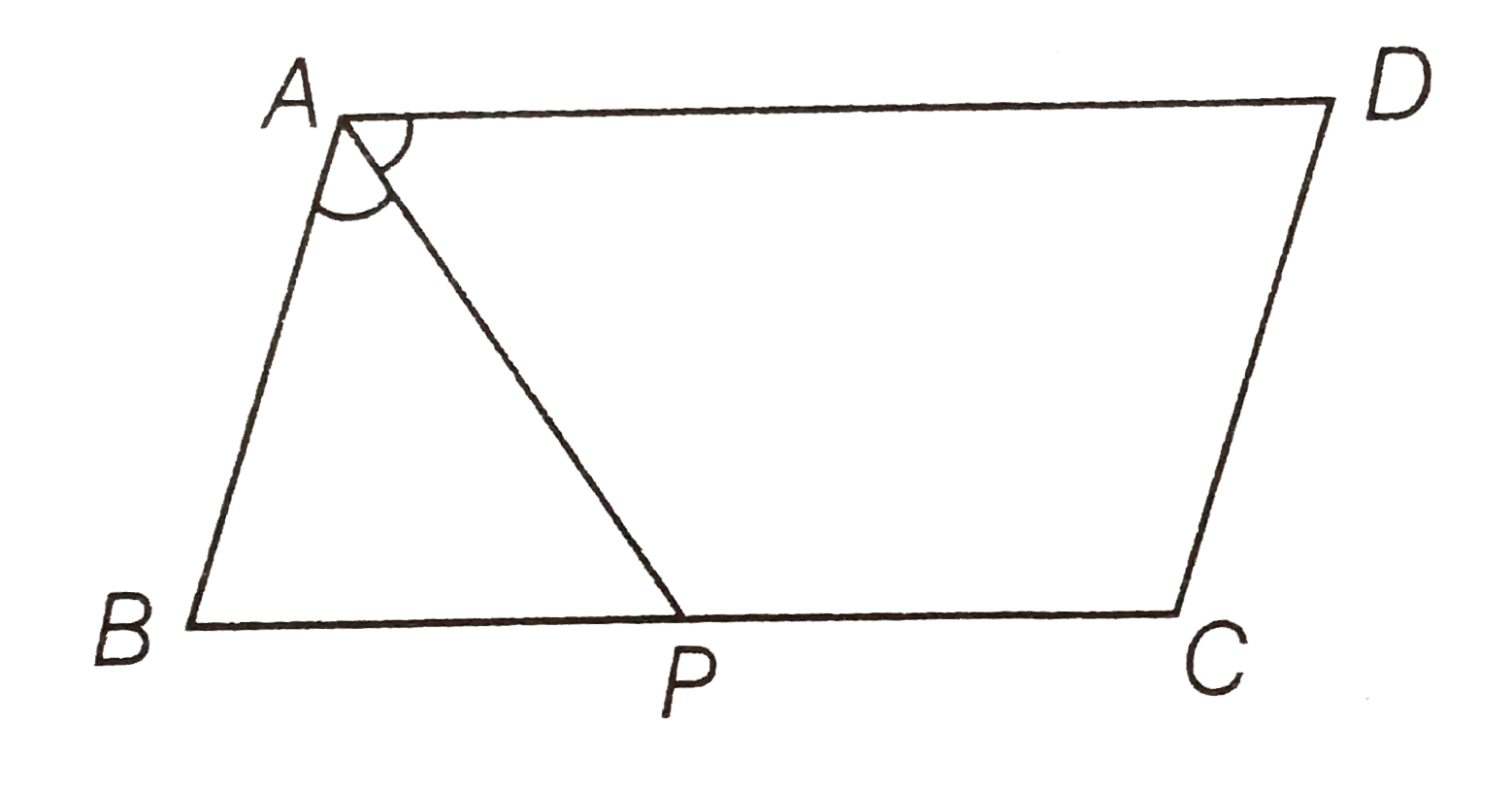
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD. ltBrgt
View Solution

