E is the mid-point of the side AD of the trapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. then
Point F trisect BC
Point F bisect BC
AB=CD
None
The correct Answer is:B
Given ABCD is a trapezium in which AB||DCandEF||AB∣∣CD.
Construction Join, the diagonal AC which intersects EF at O.
To show F is the mid-point of BC.
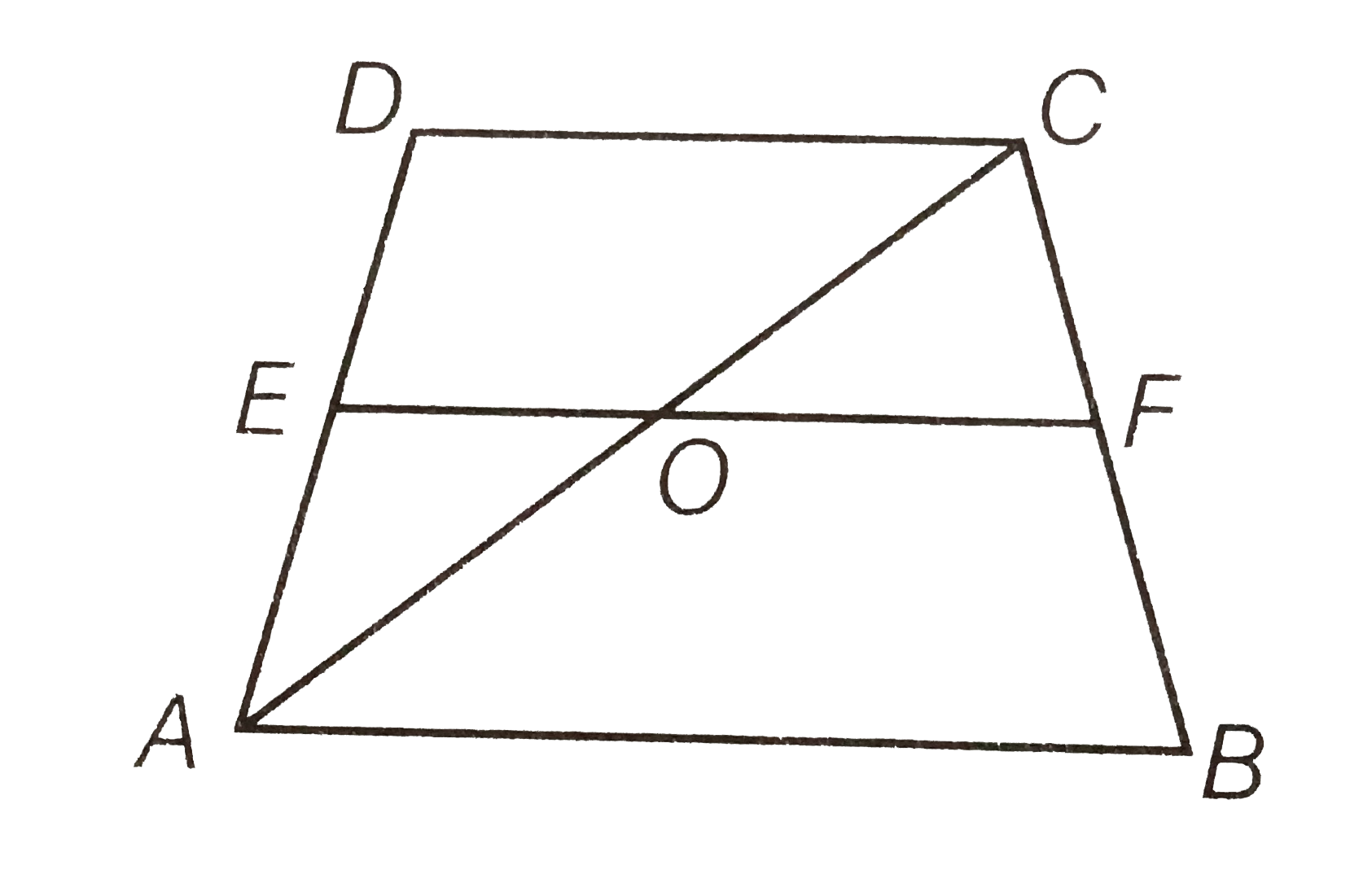
Proof Now, in ΔADC, E is the mid-point of AD and OE∣∣ CD.
Thus, by mid-point theorem, O is mid-point of AC.
Now, in ΔCBA, O is the mid-point of AC and OF ∣∣ AB.
So, by mid-point theorem, F is the mid-point of BC.
Topper's Solved these Questions
Similar Questions
P is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
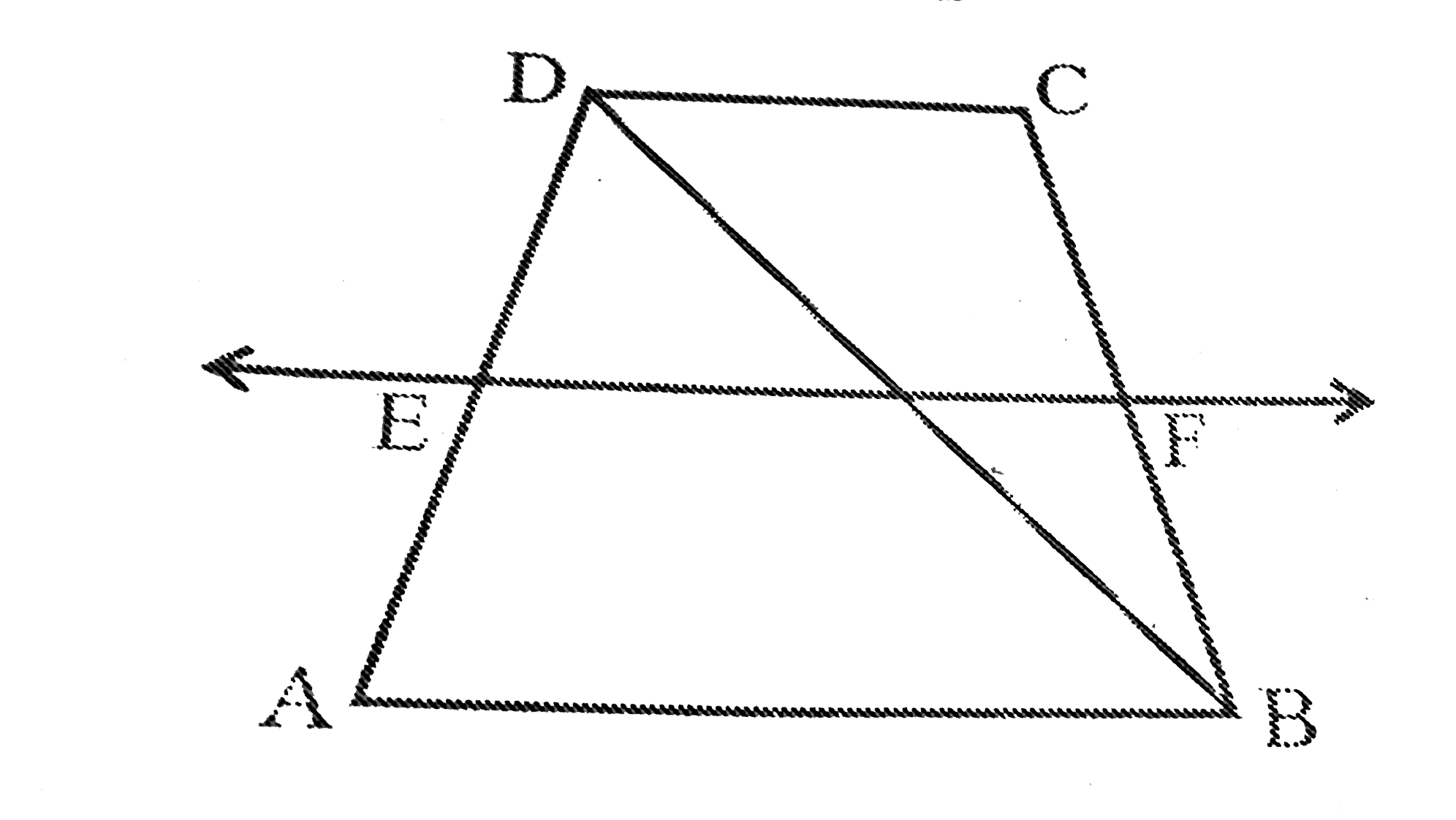
View Solution15 O is the point of intersection of the diagonals AC and BD ofa trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. rove that PO=QO ,
View SolutionABCD is a trapezium with AB || DC. E is midpoint of side AD. From point E a line is drawn parallel to AB that intersects BC at F. Show that F is midpoint of BC.
View SolutionO is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB||DC. Through O , aline segment PQ is drawn parallel to AB meeting AD in P and BC in Q, prove that PO=QO.
View SolutionP is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQ
View SolutionABCD is a trapezium in which AB ∣∣ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
View SolutionIn ΔABC, the bisector of ∠A interseats BC at D. A perpendicular to AD from B intersects AD at E. A line segment through E and parallel to AC intersects BC at G and AB at H. If AB = 26, BC = 28, AC = 30. Find the measure of DG.
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through AandC, lines are drawn parallel to BCandPA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
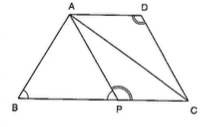
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through A and C, lines are drawn parallel to BC and PA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
View Solution
