ABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. then the quadrilateral PQRS is a
Rectangle
Square
Trapezium
None
The correct Answer is:A
Given In quadrilateral ABCD, P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively.
Also, AC⊥BD
To prove PQRS is a rectangle.
Proof Since, AC⊥BD
∴ ∠COD=∠AOD=∠AOB=∠COB=90∘ ltBrgt In ΔADC, S and R are the mid-points of AD and DC respectively, then by mid-point theorem
SR∣∣ACandSR=12AC ...(i)
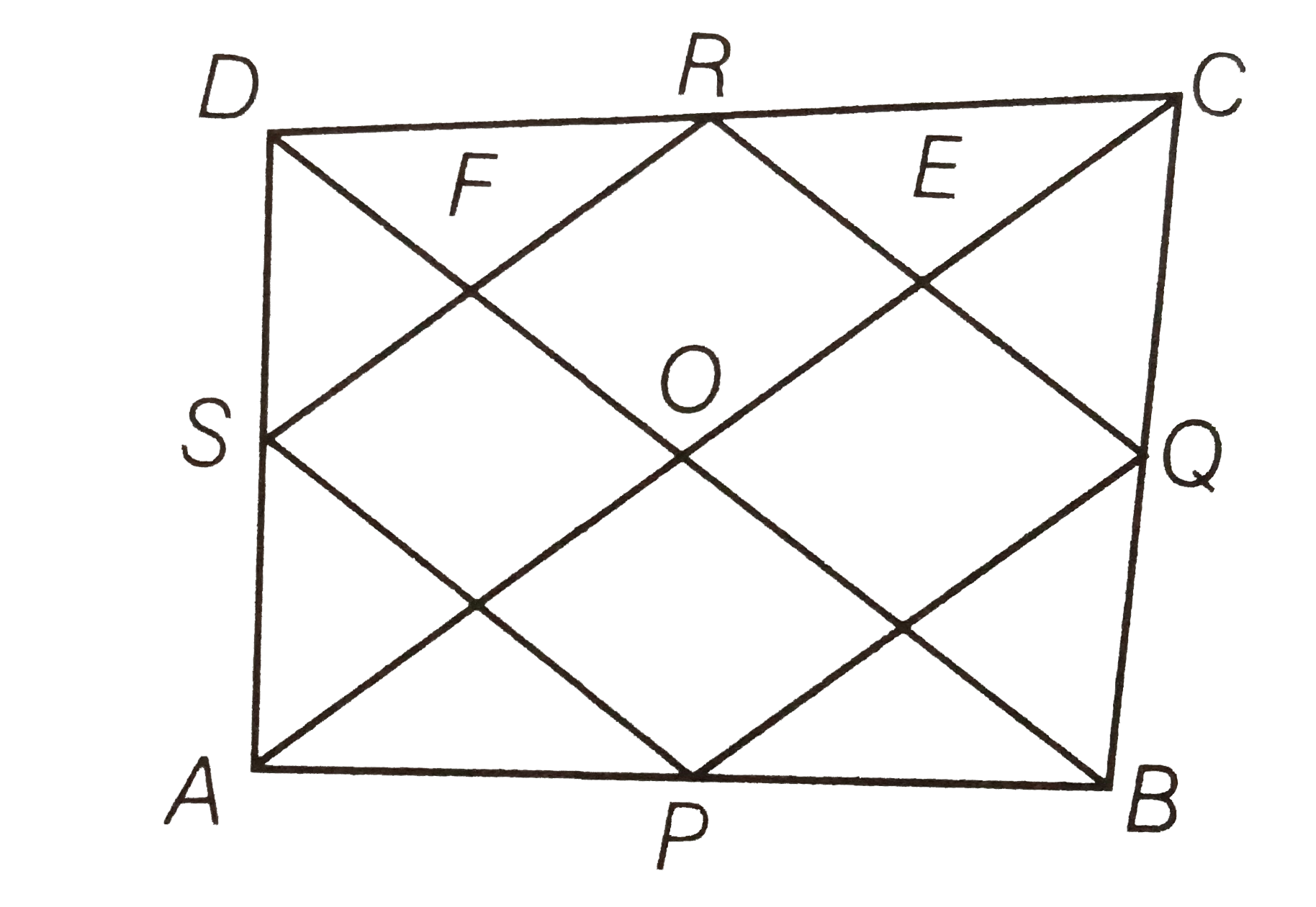
In ΔABC, P and Q are the mid-points of AB and BC respectively, then by mid-point theorem
PQ∣∣ACandPQ=12AC ...(ii)
From Eqs. (i) and (ii), PQ∣∣SRandPQ=SR=12AC ...(iii)
Similarly, SP∣∣RQandSP=RQ=12BD ...(iv)
Now, in quadrilateral EOFR, OE||FR,OF||ER
∴ ∠EOF=∠ERF=90∘ [∵∠COD=90∘⇒∠EOF=90∘]...(v)
So, PQRS is a rectangle. Hence proved.
Topper's Solved these Questions
Similar Questions
ABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View Solution
Knowledge Check
If ABCD be a rectangle and P, Q, R, S be the mid-points of AB, BC, CD and DA respectively, then the area of the quadrilateral PQRS is equal to
A13 are (ABCD)B34 area (ABCD)C12 area (ABCD)Darea (ABCD)In a triangle ABC, points P, Q and R are the mid-points of the sides AB, BC and CA respectively. If the area of the triangle ABC is 20 sq. units, find the area of the triangle PQR
A10 sq. unitsB5.3 sq. unitsC5 sq. unitsDNone of these
Let ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View Solution19. ABCD is a rectangle having length (x 1) and breadth (x- 1). If P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively, then the perimeter of quadrilateral PQRS is
View SolutionABCD is a rectangle formed by the points A(1, 1),B(1, 4),C(5, 4) and D(5, 1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? A rectangle? or a rhombus? Justify your answer.
View SolutionIf ΔABC is a equilateral triangle and P, Q, R are mid-points of sides AB, BC and CA respectively then-
View SolutionABCD is a rhombus and P,Q,R,S are the mid-points of AB,BC,CD,DA respectively. Prove that PQRS is a rectangle.
View SolutionIn the given figure, ABCDEF is a regular hexagon of side 12cm. P, Q and R are the mid points of the sides AB, CD and EF respectively. What is the area (in cm2) of triangle PQR ?
View Solution
