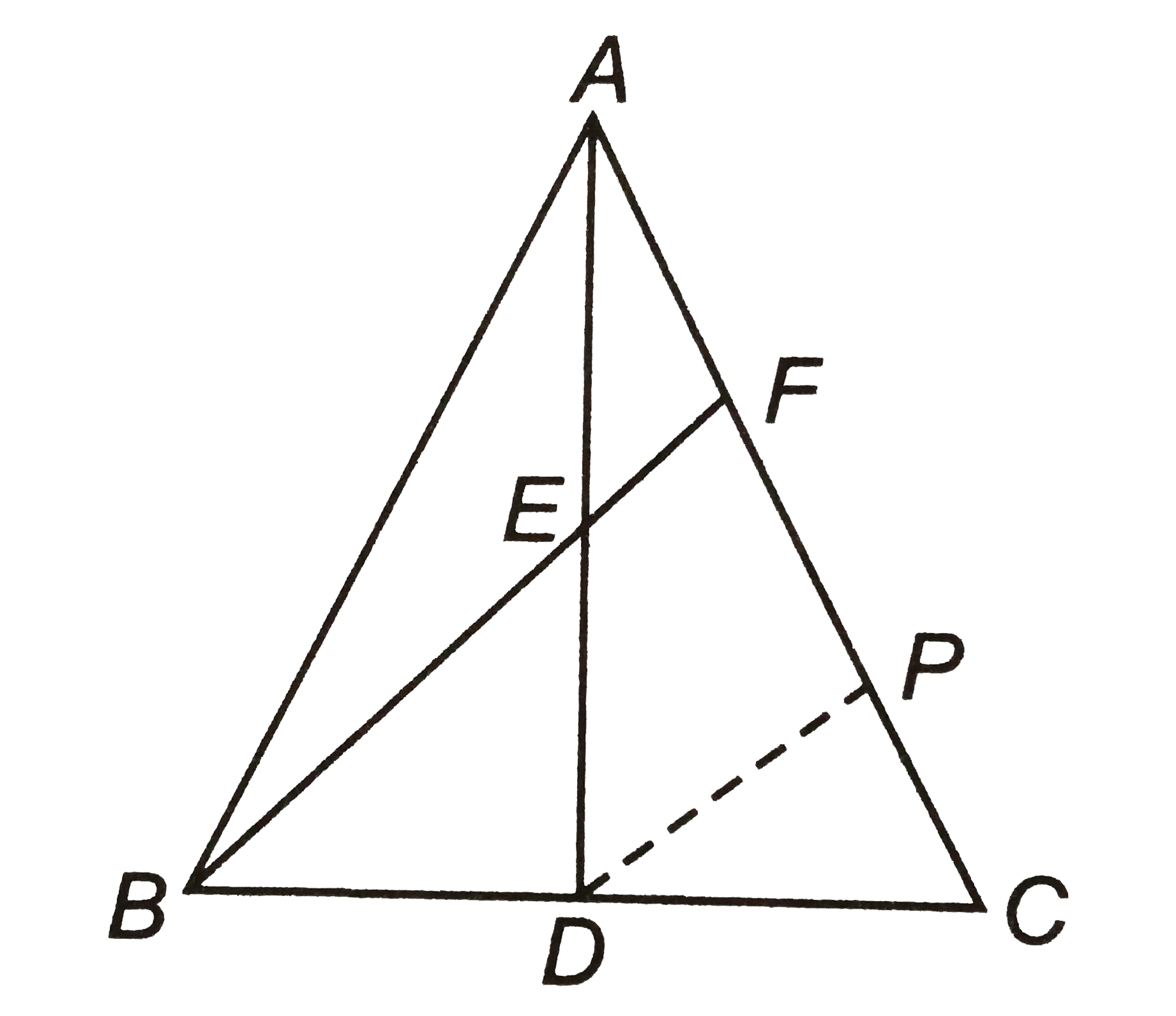
In ABC,AD is the median through A and E is the mid-point of AD. BE produced meets AC in F (Figure). Prove that AF=13AC.
Given In a ΔABC, AD is a median and E is the mid-point of AD.
Construction Draw DP||EF.
Proof In ΔADP, E is the mid-point of AD and EF||DP.
So, F is mid-point of AP. [by converse of mid-point theorem]
In ΔFBC, D is mid-point of BC and DP||BF.
So, P is mid-point of FC.
Thus, AF=FP=PC
∴ AF=13AC Hence proved.
Topper's Solved these Questions
Similar Questions
In ABC,AD is the median through A and E is the mid-point of AD . BE produced meets AC in F (Figure). Prove that AF=13AC.
View SolutionABCD is a parallelogram. AD is a produced to E so that DE=DC and EC produced meets AB produced in F. Prove that BF=BC.
View SolutionIn Figure, AD is the median and DE∣∣AB . Prove that BE is the median.
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionE is the mid-point of the median AD of ΔABC. Line segment BE meets AC at point F when produce, prove that AF=13AC.
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14ACView SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F Prove that: ar(FED)=18ar(AFC)
View SolutionIn Figure, ABC and BDE are two equilateral triangls such that D is the mid-point of BC.AE intersects BC in F. Prove that: ar ( BFE)= 2 ar (EFD)
View SolutionABCD is a parallelogram and E is the mid-point of BC, DE and AB when produced meet at F. Then AF= 32AB (b) 2 AB (c) 3 AB (c) 54 AB
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BFE)=ar(AFD)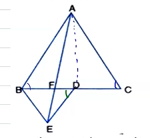
View Solution