ABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: (i) APCQ is a parallelogram. (ii) DPBQ is a parallelogram. (iii) PSQR is a parall
Given In a parallelogram ABCD, P and Q are the mid-points of AB and CD, respectively.
To show PRQS is a parallelogram.
Proof Since, ABCD is a parallelogram.
AB∣∣CD
⇒ AP∣∣QC
Also, AB=DC

12AB=12DC [dividing both sides by 2]
⇒ AP=QC [ since, P and Q are the mid-points of AB and DC]
Now, AP∣∣QCandAP=QC
Thus APCQ is a parallelogram.
∴ AQ||PCorSQ||PR ...(i)
Again, AB||DCorBP||DQ
Also, AB=DC⇒12AB=12DC [dividing both sides by 2]
⇒ BP=QD [since, P and Q are the mid-points of AB anc DC]
Now, BP∣∣QDandBP=QD
So, BPDQ is a parallelogram.
∴ PD||BQorPS||QS ...(iii)
From Eqs. (i) and (ii), SQ||RQandPS||QR
So, PRQS is a parallelogram. Hence proved.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
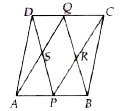
(i) APCQ is a parallelogram.
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

DPBQ is a parallelogram
View Solution
Knowledge Check
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC
ABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

PSQR is a parallelogram.
View SolutionP and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.

View SolutionABCD is a parallelogram. E and F are mid-point of side AB and CD respectively. AF and CE intersect diagonal BD at P & Q respectively. If BD = 15 cm, find PQ.

View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
(i) SR ∣∣ ACand SR=12AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH.
View SolutionABCD is a parallelogram. P and Q are mid points of BC & CD. Find the area of ΔAPQ if area of ΔABC is 12.
View Solution
