P and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.

Given: A parallelogram ABCD in which P and Q are the mid-points of the sides AB and CD respectively. AQ intersects DP at S and BQ interects CP respectively. AQ intersects DP at S and BQ intersects Cp at R.
To prove: PRQS is a parallelogram.
Proof: DC||AB (becauseopposite sides of a parallelogram are parallel)
⇒ AP||QC
DC||AB (∵opposite sides of a parallelogram are equal)
⇒ 12DC=12AB
⇒ QC=AP (∵P is mid-point of AB and Q is mid-points of CD)
⇒ APCQis a parallelogram. (∵AP||QCandQC=AP)
∴ AQ||PC (∵opposite sides of a parallelogram are parallel)
⇒ SQ||PR
Similarly, SP||QR
∴ Quadrilateral PQRS is a parallelogram.
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8b
Explore 15 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Revision Exercise (long Answer Questions)
Explore 5 Videos
- PROBABILITYBook:NAGEEN PRAKASHANChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHANChapter:STATISTICSExercise:Revision Exercise
Explore 10 Videos
Similar Questions
ABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

PSQR is a parallelogram.
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

DPBQ is a parallelogram
View Solution
Knowledge Check
X and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Then □AXCY is a ?
ATrapeziumBKiteCRhombusDParallelogramIf P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
AACB12ACC23ACD32ACIn the given figure, M is the mid-point of the side CD of the parallelogram ABCD. What is ON:OB?
 A3:2B2:1C3:1D5:2
A3:2B2:1C3:1D5:2
ABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: (i) APCQ is a parallelogram.(ii) DPBQ is a parallelogram.(iii) PSQR is a parallelogram
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
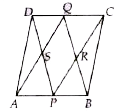
(i) APCQ is a parallelogram.
View SolutionE and F are the mid-points of the sides AB and CD of a parallelogram ABCD. Prove that the line segment AF and CE trisects BD in three equal parts.
View SolutionIf P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the diagonal AC in its points of trisection which are also the points of trisection of DP and BQ respectively.
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F . Show that ΔABE~ΔCFB .
View Solution

