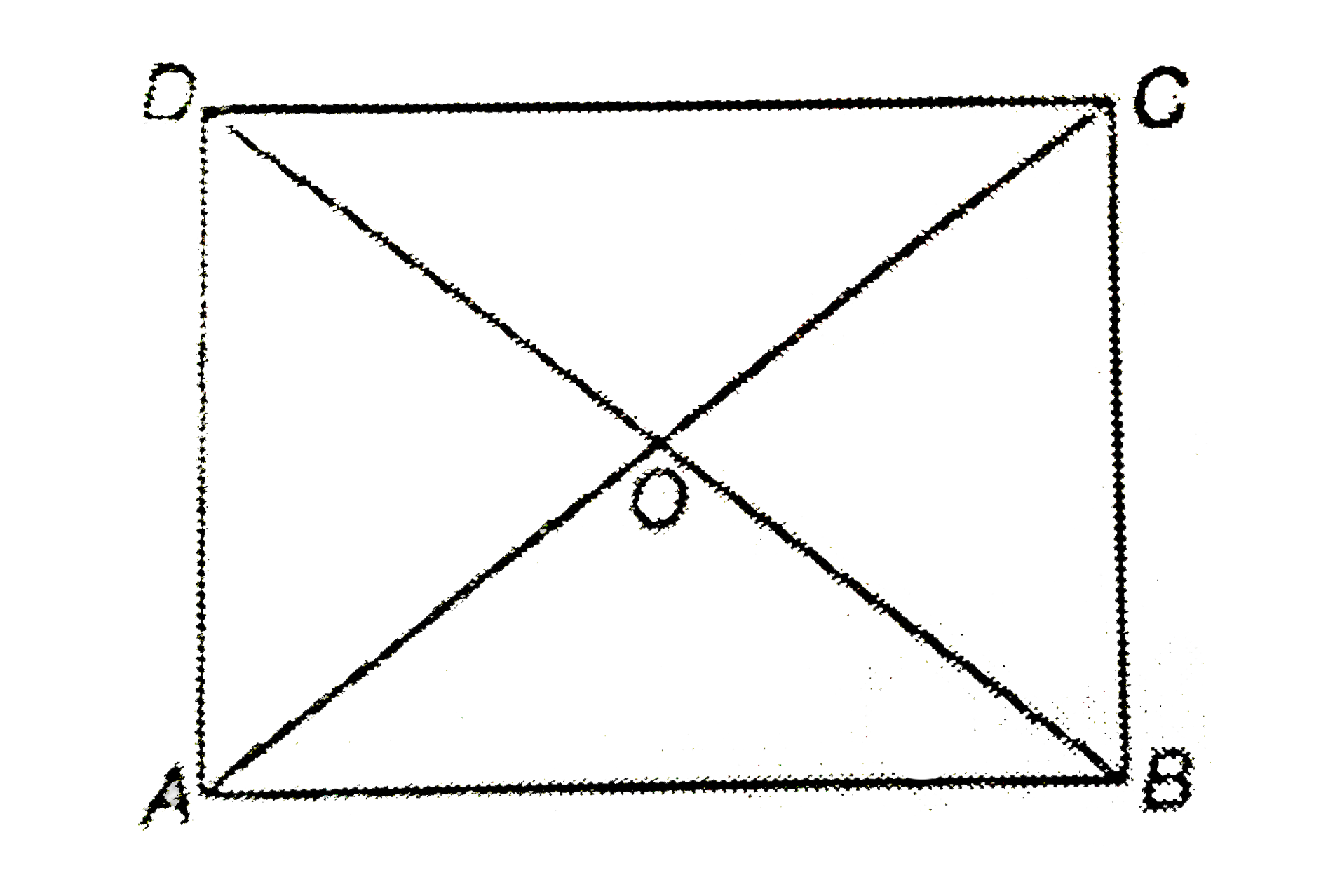
ABCD is a rectangle in which diagonal BD bisects ∠B. then ABCD is a
Rectangle
Rhombus
Parallelogram
Square
The correct Answer is:D
Given In a rectangle ABCD, diagonal BD bisects ∠B.
Construct Join AC.
To show ABCD is a square.
Proof
In ΔBAD and ΔBCD, ∠ABD=∠CBD [given]
∠A=∠C [each 90∘]
and BD=BD [common side]
∴ ΔBAD≅ΔBCD [by AAS congruence rule]
∴ AB=BC
and AD=CD [by CPCT rule]...(i)
But in rectangle ABCD, opposite sides are equal.
∴ AB=CD
and BC=AD ...(ii)
From Eqs. (i) and (ii),
AB=BC=CD=DA
So, ABCD is a square. Hence proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
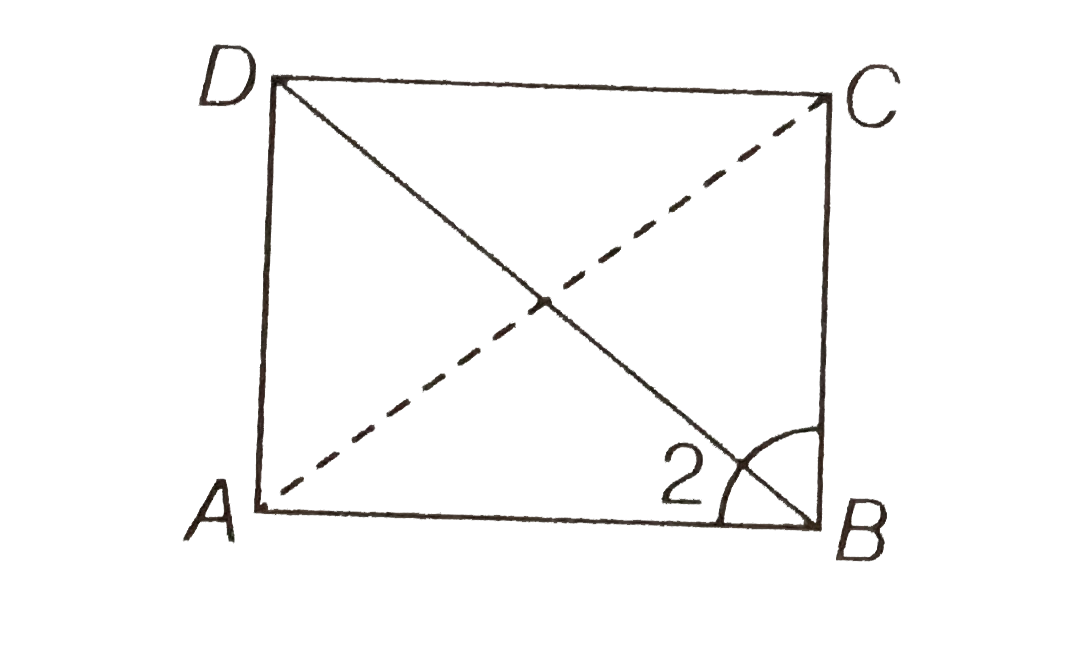
If in a rectangle ABCD, diagonal AC bisect ∠A as well as ∠C then ABCD is a
AParallelogramBsquareCRhombusDTrapeziumIn the given figure, ABCD is a rectangle whose diagonals AC and BD intersect at 0. If ∠OAB=28∘, then ∠OBC is equal to
 A72∘B50∘C62∘D75∘
A72∘B50∘C62∘D75∘In the given figure, ABCD is a ||gm in which diagonals AC and BD intersect at O. If ar(||gm ABCD) is 52cm2 then the ar(△AOB)=?
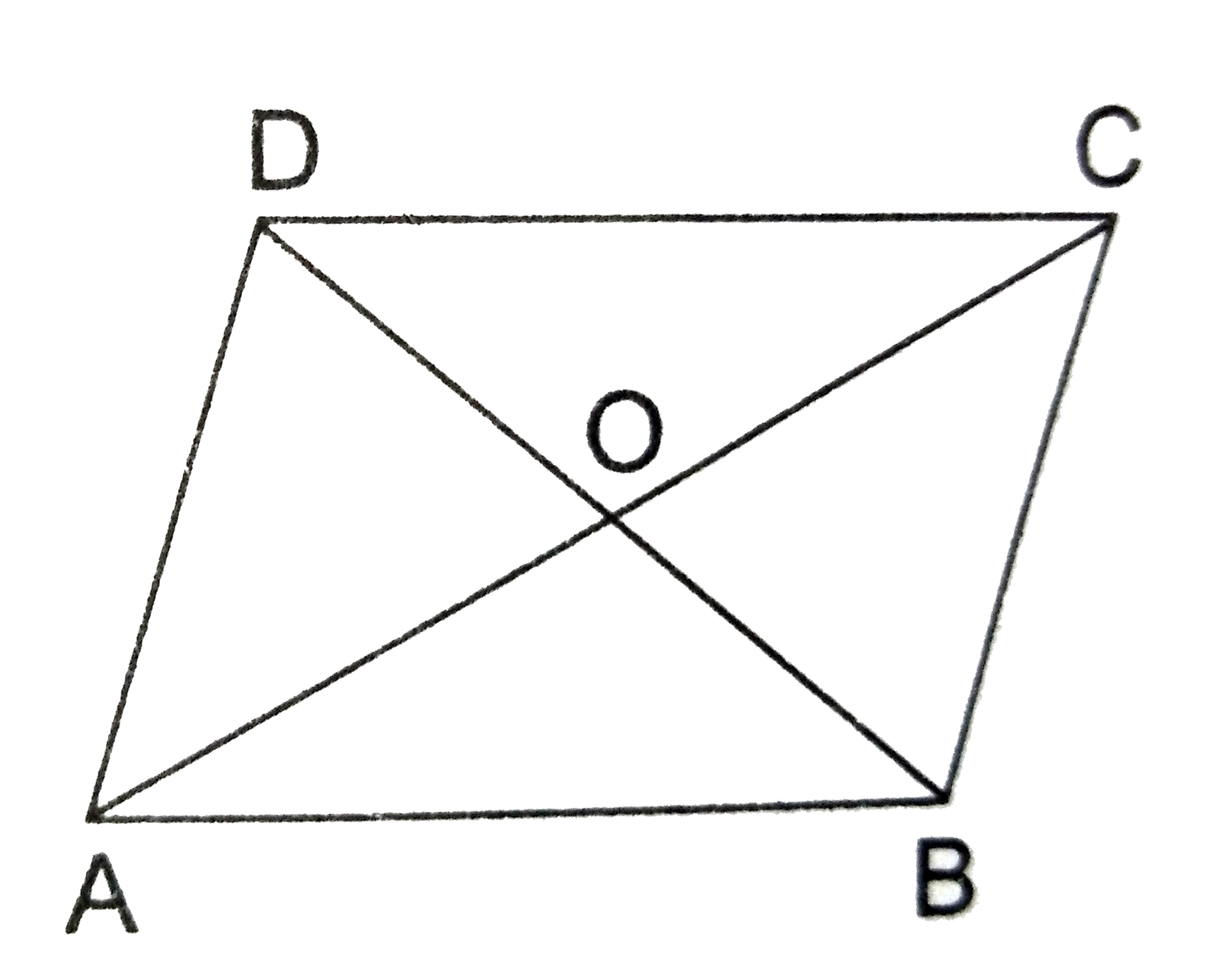 A26cm2B18.5cm2C39cm2D13cm2
A26cm2B18.5cm2C39cm2D13cm2
ABCD is a rectangle in which diagonal AC bisects ∠Aas well as ∠C. Show that:
(i) ABCD is a square
(ii) diagonal BD bisects ∠Bas well as ∠D..
View SolutionIn the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB=28∘, find ∠OBC.
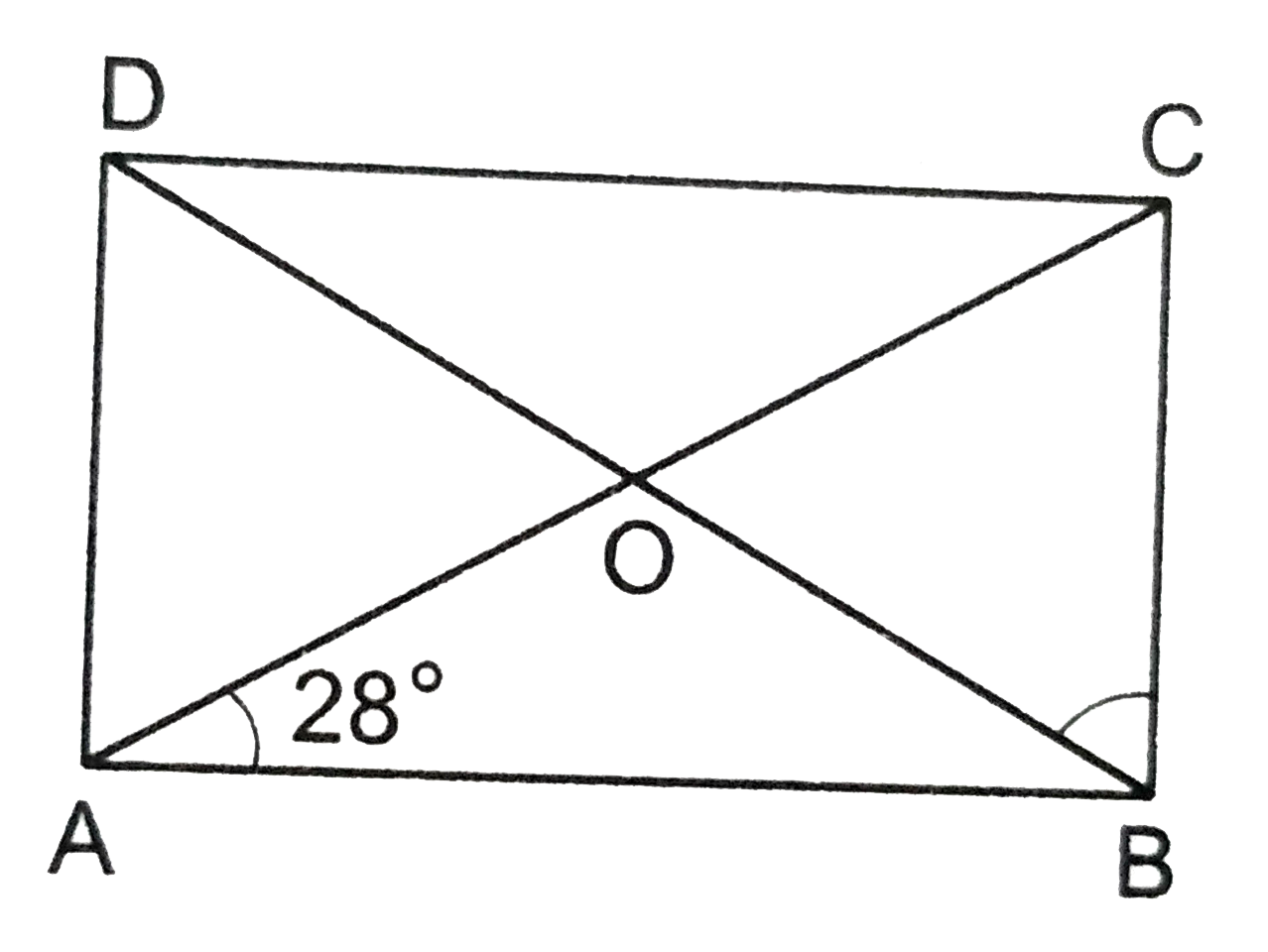
View SolutionABCD is a rectangle. The diagonals AC and BD intersect at O. If AB = 32 cm and AD = 24 cm, then what is OD equal to ?
View SolutionThree statements are given below:
I. In a rectangle ABCD, the diagonal AC bisects ∠A as well as ∠C.
II. In a square ABCD, the diagonal AC bisects ∠A as well as ∠C.
III. In a rhombus ABCD, the diagonal AC bisects ∠A as well as ∠C.
Which is true?
View SolutionABCD is a quadrilateral in which diagonal BD = 64 cm. AL⊥BD and CM⊥BD, such that AL=13.2cm and CM=16.8cm. The area of the quadrilateral ABCD is square centimeters is :
View Solution