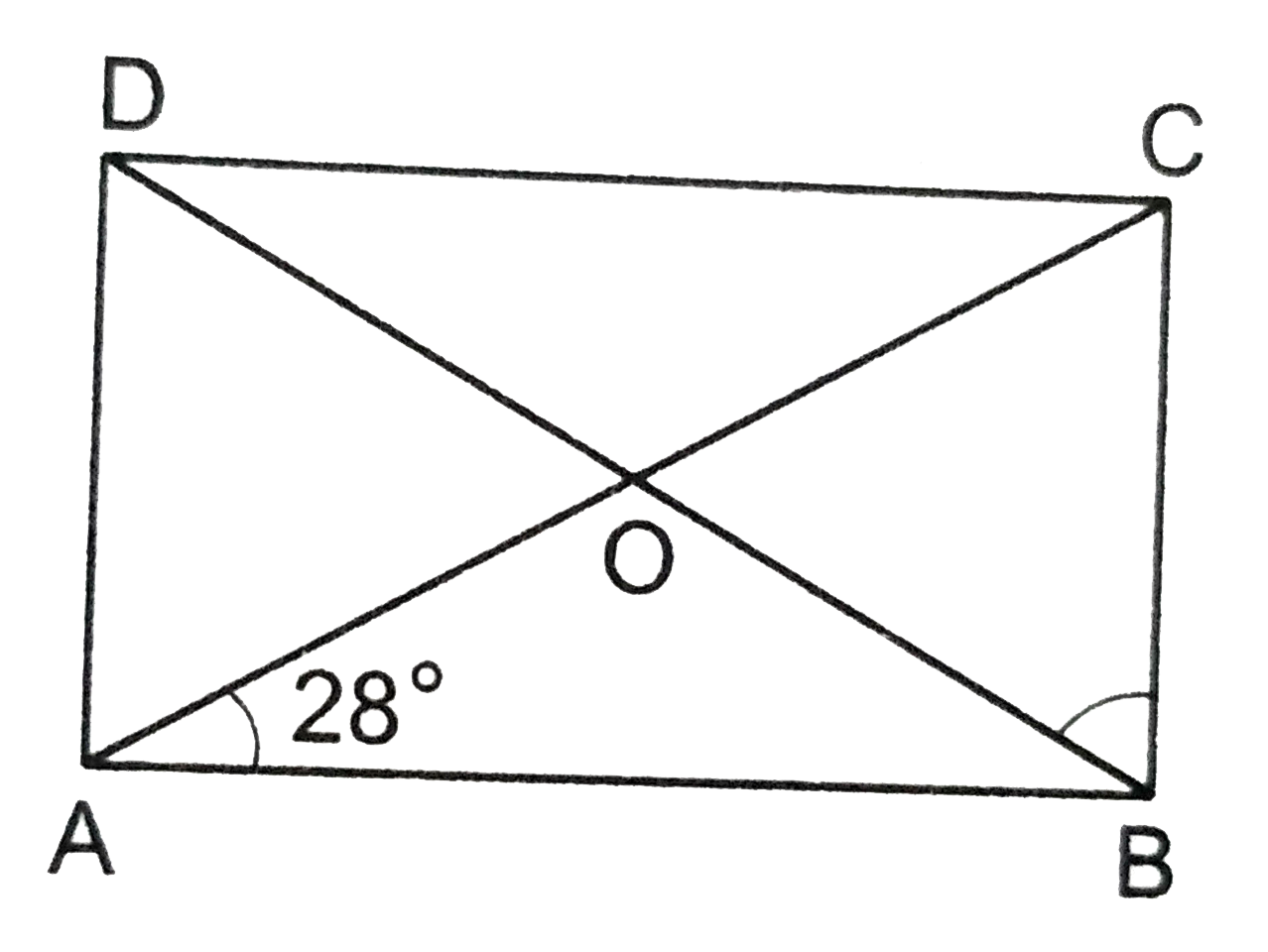
In the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB=28∘, find ∠OBC.
Video Solution
Text Solution
We know that the diagonals of a rectangle are equal and bisect each other.
∴OA=OB⇒∠OBA=∠OAB=28∘.
Also, each angle of a rectangle measures 90∘.
∴∠ABC=90∘⇒∠OBA+∠OBC=90∘
∴28∘+∠OBC=90∘⇒∠OBA=(90∘−28∘)=62∘.
|
Topper's Solved these Questions
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:EXAMPLE
Explore 32 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Exercise 10 A
Explore 10 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 10 Videos
Similar Questions
Knowledge Check
In the given figure, ABCD is a rectangle whose diagonals AC and BD intersect at 0. If ∠OAB=28∘, then ∠OBC is equal to
 A72∘B50∘C62∘D75∘
A72∘B50∘C62∘D75∘In figure, ABCD is a rectangle in which diagonal D AC is produced to E. If ∠ECD=146∘, find ∠AOB.
 A11∘B115∘C112∘DNone of these
A11∘B115∘C112∘DNone of theseIn the given figure, ABCD is a ||gm in which diagonals AC and BD intersect at O. If ar(||gm ABCD) is 52cm2 then the ar(△AOB)=?
 A26cm2B18.5cm2C39cm2D13cm2
A26cm2B18.5cm2C39cm2D13cm2
The diagonals of rectangle ABCD intersect at O . If ∠AOD=40∘ , then find ∠OAD
View SolutionIn a rectangle ABCD, diagonals AC and BD intersect at O. If ∠OAB=35∘, find :
(a)∠ABC(b)∠ABO(c)∠CO(d)∠BOC)
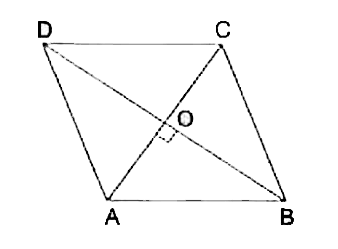
View SolutionIn the adjacent figure , ABCD is a rhombus whose diagonals AC and BD intersect at a point O. If side AB=10 cm and diagonal BD=16 cm , find the length of diagonal AC.
View SolutionABCD is a rectangle. The diagonals AC and BD intersect at O. If AB = 32 cm and AD = 24 cm, then what is OD equal to ?
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View Solution
