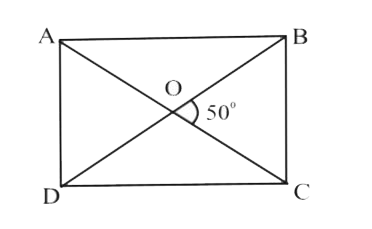
The diagonals of rectangle ABCD intersect at O . If ∠AOD=40∘ , then find ∠OAD
The correct Answer is:70∘
To solve the problem, we need to find the angle ∠OAD in rectangle ABCD where the diagonals intersect at point O and ∠AOD=40∘.
1. Understanding the Properties of a Rectangle:
- In a rectangle, the diagonals bisect each other and are equal in length. Therefore, OA=OC and OB=OD.
2. Identifying Angles:
- We know that ∠AOD=40∘. Since O is the intersection point of the diagonals, we can also state that ∠BOC is equal to ∠AOD because diagonals of a rectangle bisect each other.
3. Using the Triangle Angle Sum Property:
- In triangle OAD, the sum of the angles is 180∘. Therefore, we can write:
∠OAD+∠AOD+∠ODA=180∘
4. Identifying Angles in Triangle OAD:
- Since OA=OD (as mentioned earlier), triangle OAD is isosceles. This means that the angles opposite to the equal sides are equal:
∠OAD=∠ODA
- Let's denote ∠OAD=∠ODA=x.
5. Setting Up the Equation:
- Now we can substitute into the triangle angle sum equation:
x+40∘+x=180∘
- This simplifies to:
2x+40∘=180∘
6. Solving for x:
- Subtract 40∘ from both sides:
2x=180∘−40∘=140∘
- Now divide by 2:
x=140∘2=70∘
7. Conclusion:
- Therefore, ∠OAD=70∘.
Final Answer:
∠OAD=70∘
- In a rectangle, the diagonals bisect each other and are equal in length. Therefore, OA=OC and OB=OD.
- We know that ∠AOD=40∘. Since O is the intersection point of the diagonals, we can also state that ∠BOC is equal to ∠AOD because diagonals of a rectangle bisect each other.
- In triangle OAD, the sum of the angles is 180∘. Therefore, we can write:
∠OAD+∠AOD+∠ODA=180∘
- Since OA=OD (as mentioned earlier), triangle OAD is isosceles. This means that the angles opposite to the equal sides are equal:
∠OAD=∠ODA
- Let's denote ∠OAD=∠ODA=x.
- Now we can substitute into the triangle angle sum equation:
x+40∘+x=180∘
- This simplifies to:
2x+40∘=180∘
- Subtract 40∘ from both sides:
2x=180∘−40∘=140∘
- Now divide by 2:
x=140∘2=70∘
- Therefore, ∠OAD=70∘.
∠OAD=70∘
Topper's Solved these Questions
- CHALLENGING QUESTIONS Book:TARGET PUBLICATIONChapter:CHALLENGING QUESTIONS Exercise:SURFACE AREA AND VOLUME
Explore 25 Videos
- CHALLENGING QUESTIONS Book:TARGET PUBLICATIONChapter:CHALLENGING QUESTIONS Exercise:CHAPTER-1 :Linear Equations in Two Variable
Explore 6 Videos
- CHALLENGING QUESTIONS Book:TARGET PUBLICATIONChapter:CHALLENGING QUESTIONS Exercise:TRIANGLES
Explore 15 Videos
- BOARD QUESTION PAPER: MARCH 2019Book:TARGET PUBLICATIONChapter:BOARD QUESTION PAPER: MARCH 2019Exercise:(Solve the following questions (Any one):
Explore 4 Videos
- CIRCLEBook:TARGET PUBLICATIONChapter:CIRCLEExercise:Chapter Assessment
Explore 9 Videos
Similar Questions
Knowledge Check
The diagonals of rectangle ABCD intersect each other at O. If ∠BOC=44∘ , then the value of ∠OAD will be
A120∘B68∘C90∘D44∘
The diagonals of a rectangular ABCD intersect at O. If ∠BOC=68∘, then find ∠ODA

View SolutionThe diagonals of a rectangle ABCD intersect in O. if angleBOC=68∘, find angle ODA
View SolutionThe diagonals of a rectangle ABCD intersects at O. If ∠BOC=70∘. find ∠ODA.
View SolutionThe diagonals of a rectangle ABCD intersect in O. If ∠BOC=680, find ∠ODA.
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=44∘, find ∠OAD.
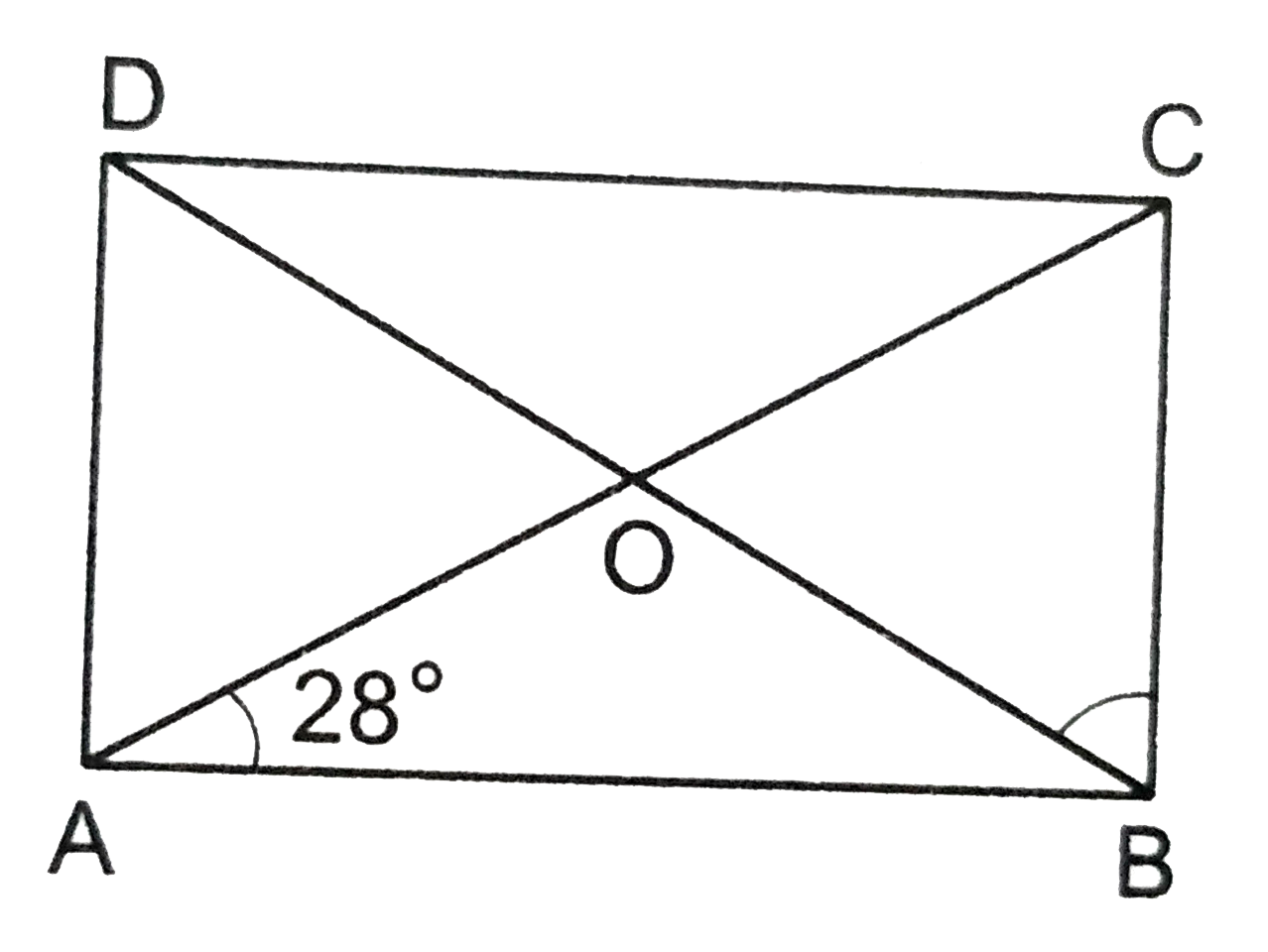
View SolutionIn the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB=28∘, find ∠OBC.
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=440, find ∠OAD.
View Solution