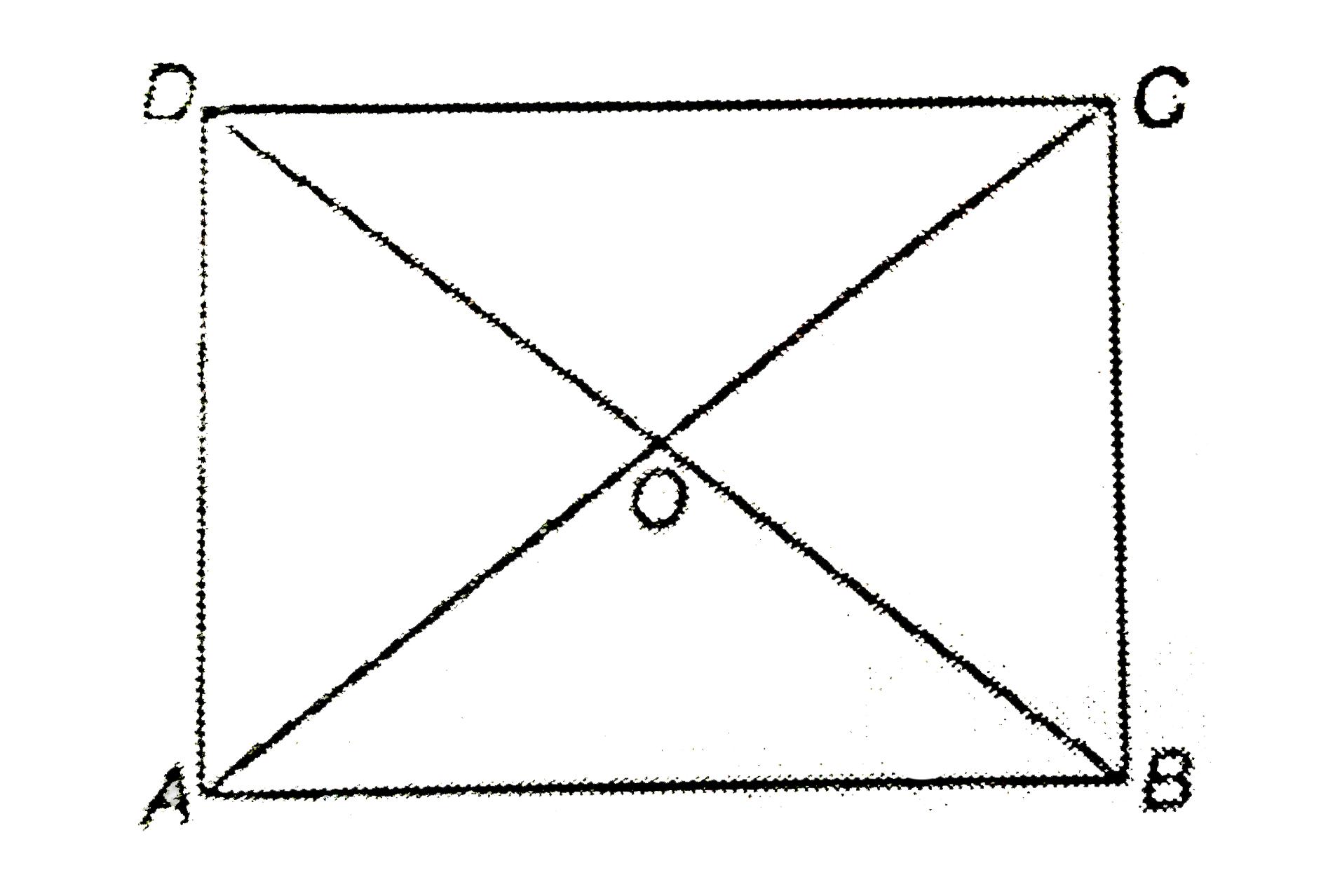
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal AD bisects ∠B
Video Solution
Text Solution
ABCD is a reactangle.
∴ AB=CDandBC=AD ...(1)
To prove : (1) ABCD is a square.
i.e., AB=BC=CD=DA
(ii) Diagonal AD bisects ∠B as well as ∠D.
Proof : (i) In ΔABCDandΔABC, transversal interects
∵⎧⎪⎨⎪⎩∠DAC=∠BAC(given)∠DCA=∠BCA(given)AC=CA(common)
∴ ΔADC≅ΔABC (by ASA rule)
∴ AD=AB (c.p.c.t.)
and CD=BC ...(2)
Hence, from eqs. (1) and (2), we get
AB=BC=AD=CD
∴ ABCD is a square.
(ii) In ΔAOBandΔCOB
∵⎧⎪⎨⎪⎩AB=BC(side of square)BO=OB(common)OA=OC(∵diagonals of square bisect each other)
∴ ΔAOB≅ΔCOB (by SSS rule)
∴ ∠OBA=∠OBC (c.p.c.t)
This shows that BO or BD bisect ∠B.
Similarly, in ΔAODandΔCOD
∵⎧⎪⎨⎪⎩AD=CD(side of square)OD=DO(common)OA=OC(∵diagonals of square bisect each other)
∴ ΔAOD≅ΔCOD (by SSS rule)
∴ ∠ADO=∠CDO
This shows that DO or DB bisect ∠D.
|
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8b
Explore 15 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Revision Exercise (long Answer Questions)
Explore 5 Videos
- PROBABILITYBook:NAGEEN PRAKASHANChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHANChapter:STATISTICSExercise:Revision Exercise
Explore 10 Videos
Similar Questions
Knowledge Check
If in a rectangle ABCD, diagonal AC bisect ∠A as well as ∠C then ABCD is a
AParallelogramBsquareCRhombusDTrapeziumThree statements are given below:
I. In a rectangle ABCD, the diagonal AC bisects ∠A as well as ∠C.
II. In a square ABCD, the diagonal AC bisects ∠A as well as ∠C.
III. In a rhombus ABCD, the diagonal AC bisects ∠A as well as ∠C.
Which is true?AI onlyBII and IIICI and IIIDI and IIABCD is a quadrlateral in which BD and AC are diagonals then
AAB+BC+CD+AD<AC+BDBAB+BC+CD+DA>AC+BDCAB+BC+CD+DA=AC+BDDAB+BC+CD+DA>2(AC+BD)
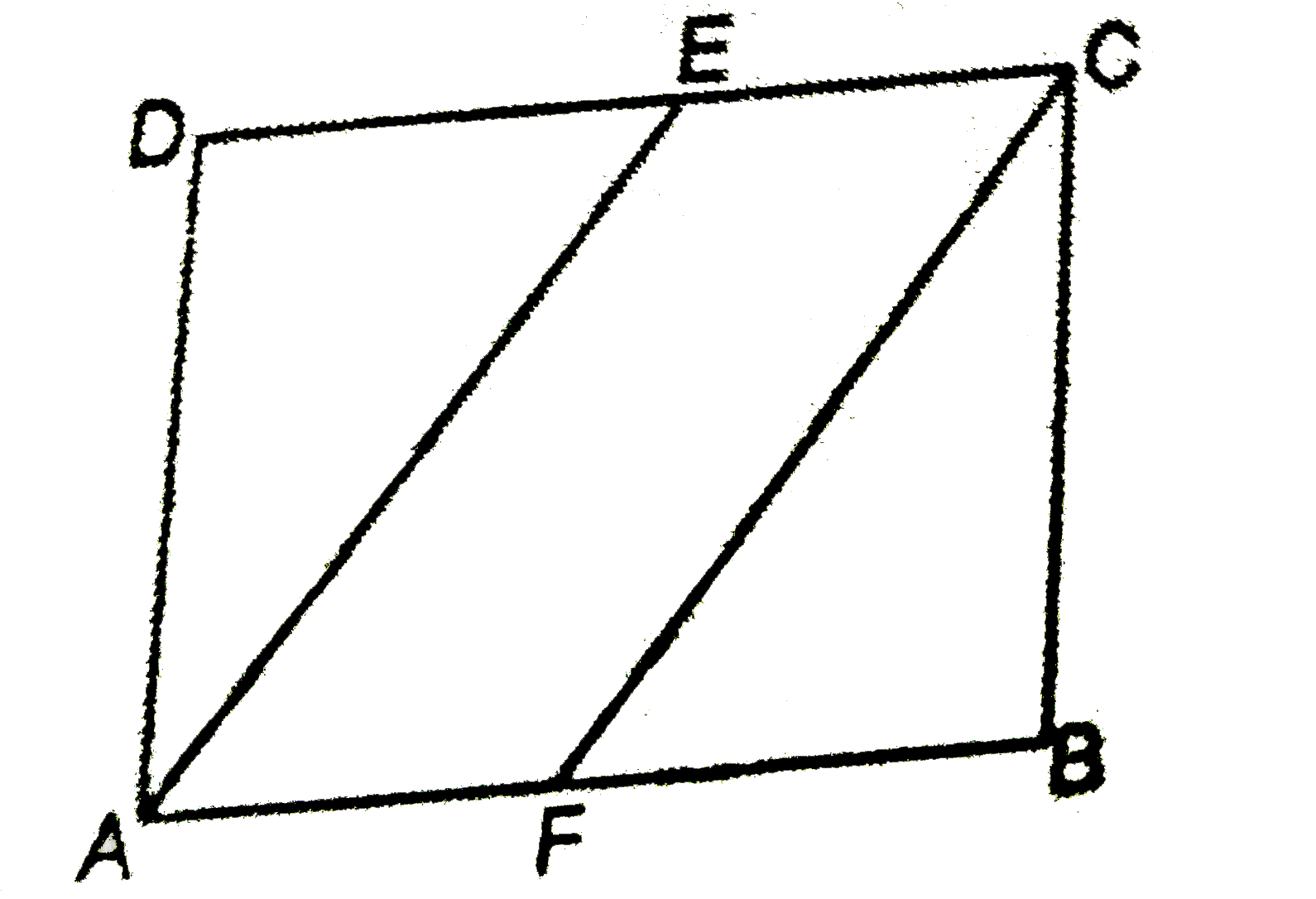
ABCD is a parallelogram and AE and CF bisect ∠Aand∠C respectively. Prove that AE||FC.
View SolutionABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠Cand diagonal BD bisects ∠B as well as ∠D.
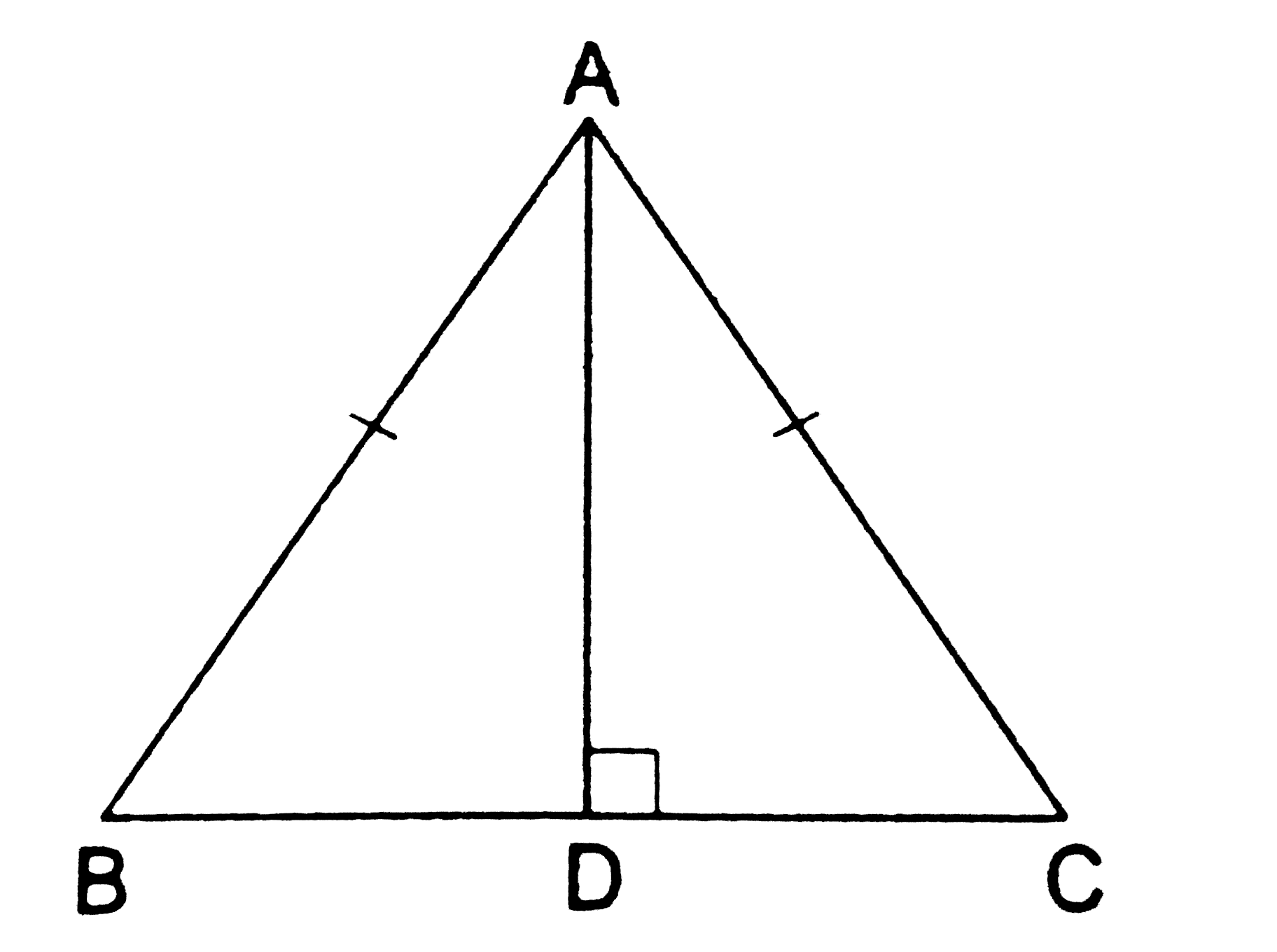
View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
View SolutionABCD is a parallelogram in which ∠A=78∘. Compute ∠B,∠Cand∠D.
View SolutionIn figure, ABCD is a rectangle in which diagonal D AC is produced to E. If ∠ECD=146∘, find ∠AOB.

View Solution

