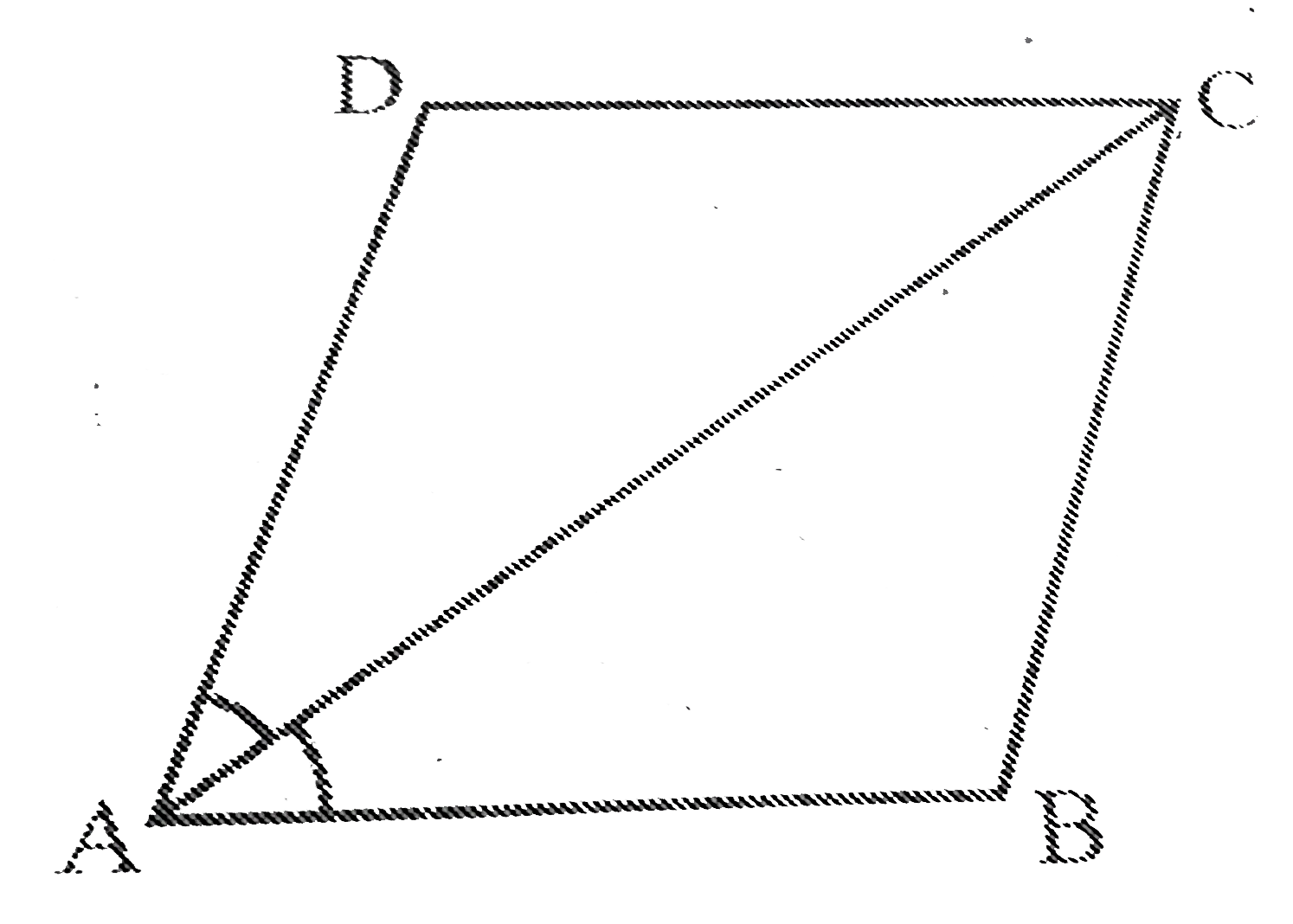
Diagonal AC of a paraleligram ABCD bisects ∠A (sec figure). Show that:
(i) it bisects ∠C also (ii) ABCD is a rhombus.
Video Solution
Text Solution
Given, diagonal AC of a parallelogram ABCD bisects ∠A.
(i) We have
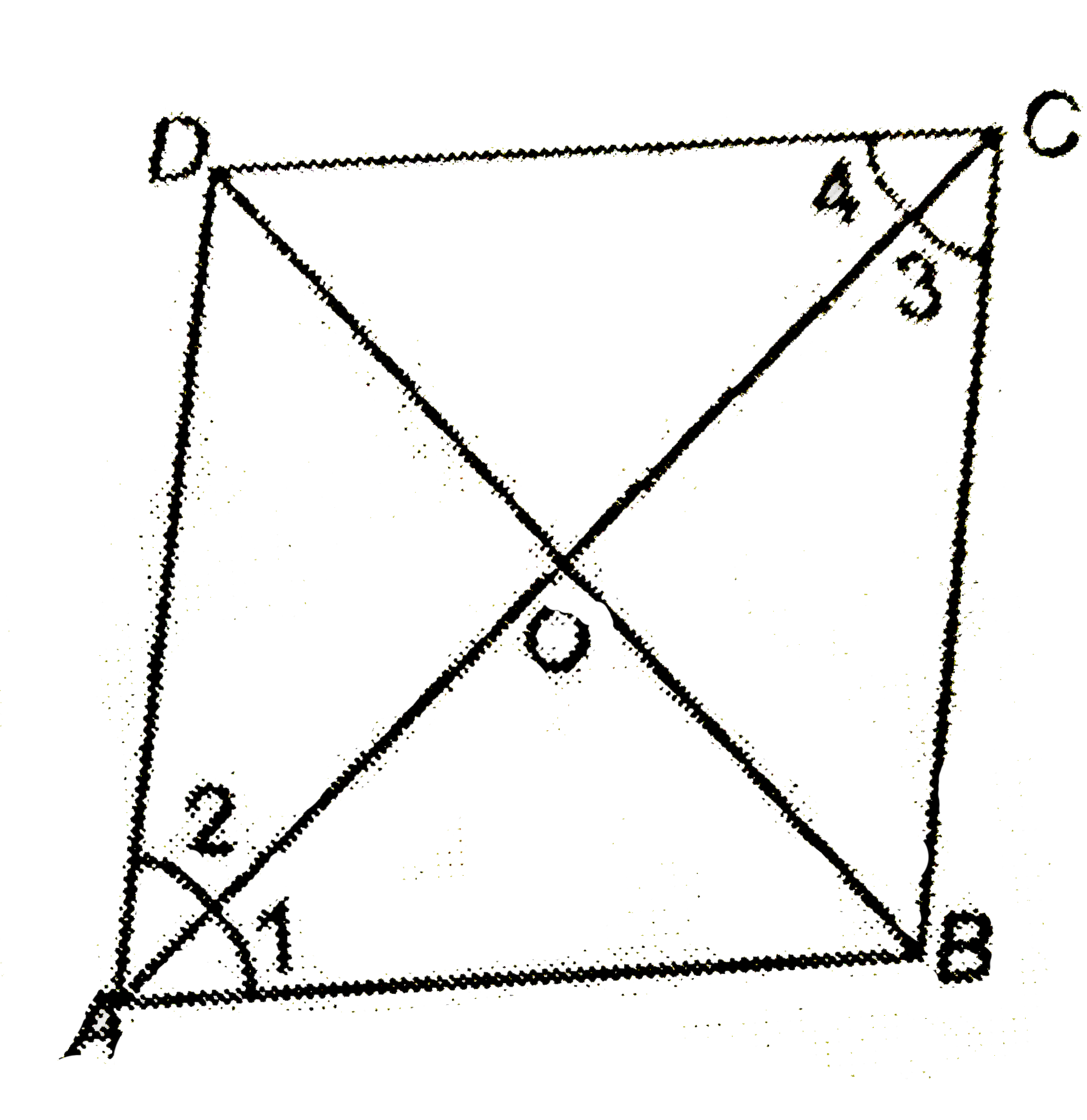
∠1=∠2 (given)...(1)
But ∠1=∠4(alternate angles asAB||DC)...(2)
and ∠2=∠3 (alternate angles asAD||BC)...(3)
∴ Diagonal AC also bisects ∠C.
(ii) Since ∠1=∠2 (given)
and ∠2=∠3 (alternate angles as||BC)
∴ ∠1=∠3
⇒ AB=BC (sides opposite to equal angles are equal)
Now, since djacent sides of a parallelogram are equal.
∴ □ABCD is a rhombus.
|
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8b
Explore 15 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Revision Exercise (long Answer Questions)
Explore 5 Videos
- PROBABILITYBook:NAGEEN PRAKASHANChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHANChapter:STATISTICSExercise:Revision Exercise
Explore 10 Videos
Similar Questions
Knowledge Check
The diagonal BD of a quadrilateral ABCD bisects ∠Band∠D, then :
 AABCD=ADBCBADAB=BCCDCABBC=ADCDDAB=AD×BC
AABCD=ADBCBADAB=BCCDCABBC=ADCDDAB=AD×BCIf ABCD is a parallelogram then ∠A−∠C=
A180∘B0∘C360∘D90∘In a parallelogram ABCD, the bisector of anl≥A also bisects BC at E, find the AD.
AABB2ABC3ABD12AB
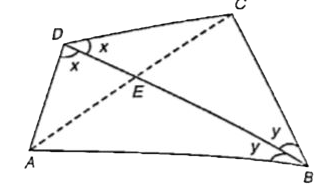
In Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
View SolutionIf diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle. Also, prove that it is a rhombus.
View Solutionif diagonals of a parallelogram bisect each other,prove that its a rhombus
View SolutionIn the figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.
View SolutionIn parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
View Solution