Question

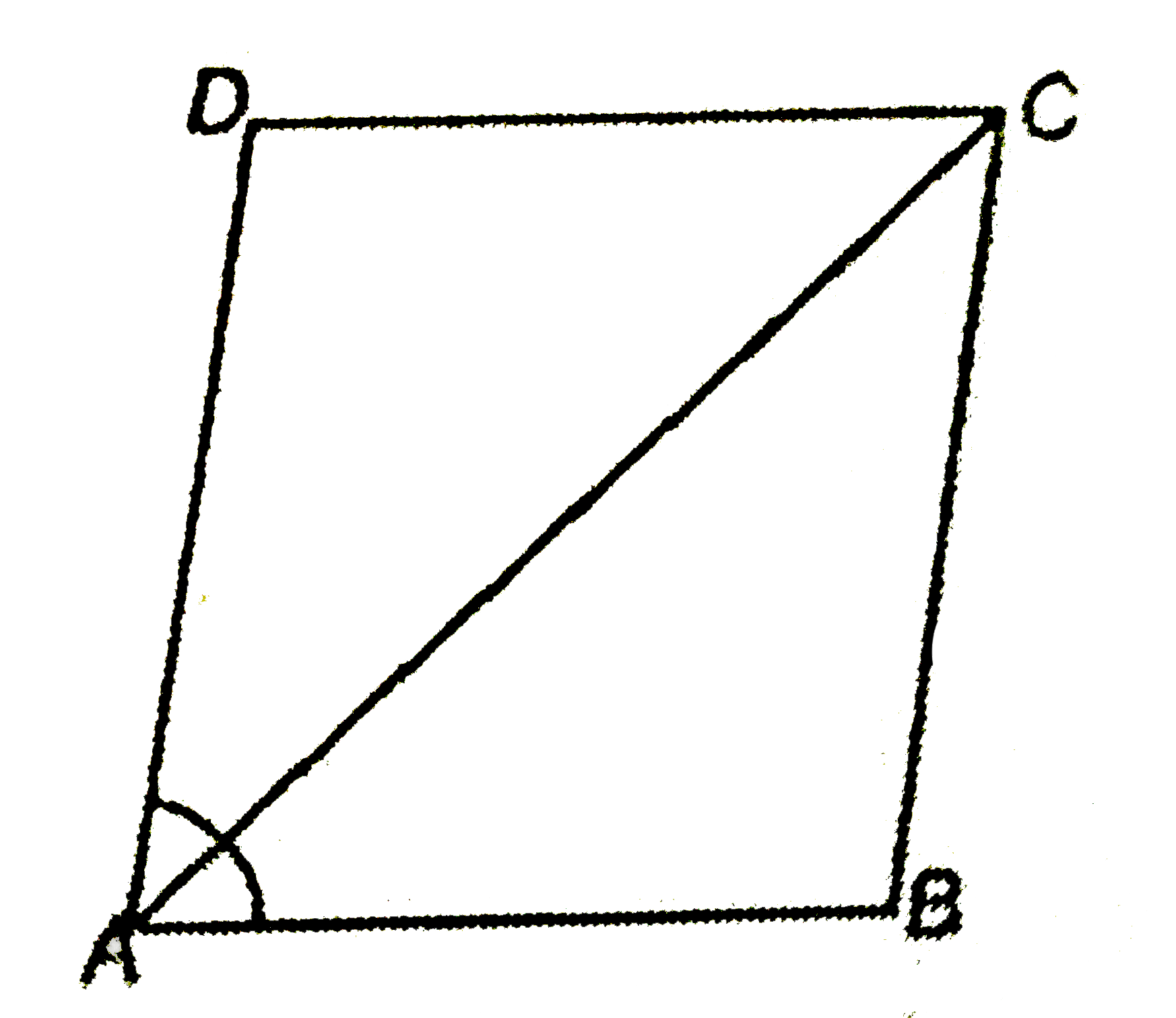
Diagonal AC of a parallelogram ABCD bisects $\angle A$. Show that
(i) it bisects $\angle C$ also,
(ii) ABCD is a rhombus.

Explanation

Given: The diagonal AC of a parallelogram ABCD bisects ∠A.


We can use alternate interior angles property to show that the diagonal AC bisects ∠C and by showing all sides are equal, it can be proved ABCD is a rhombus.



i) ABCD is a parallelogram.


`∠DAC = ∠BCA` (Alternate interior angles) ....................(1)


`∠BAC = ∠DCA` (Alternate interior angles) ....................(2)


However, it is given that AC bisects `∠A`.


`∠DAC = ∠BAC ` ....................(3)


From equations (1), (2), and (3), we obtain

`
∠DCA = ∠BAC = ∠DAC = ∠BCA` ....................(4)


Thus, `∠DCA = ∠BCA`


Hence, `AC` bisects `∠C`.


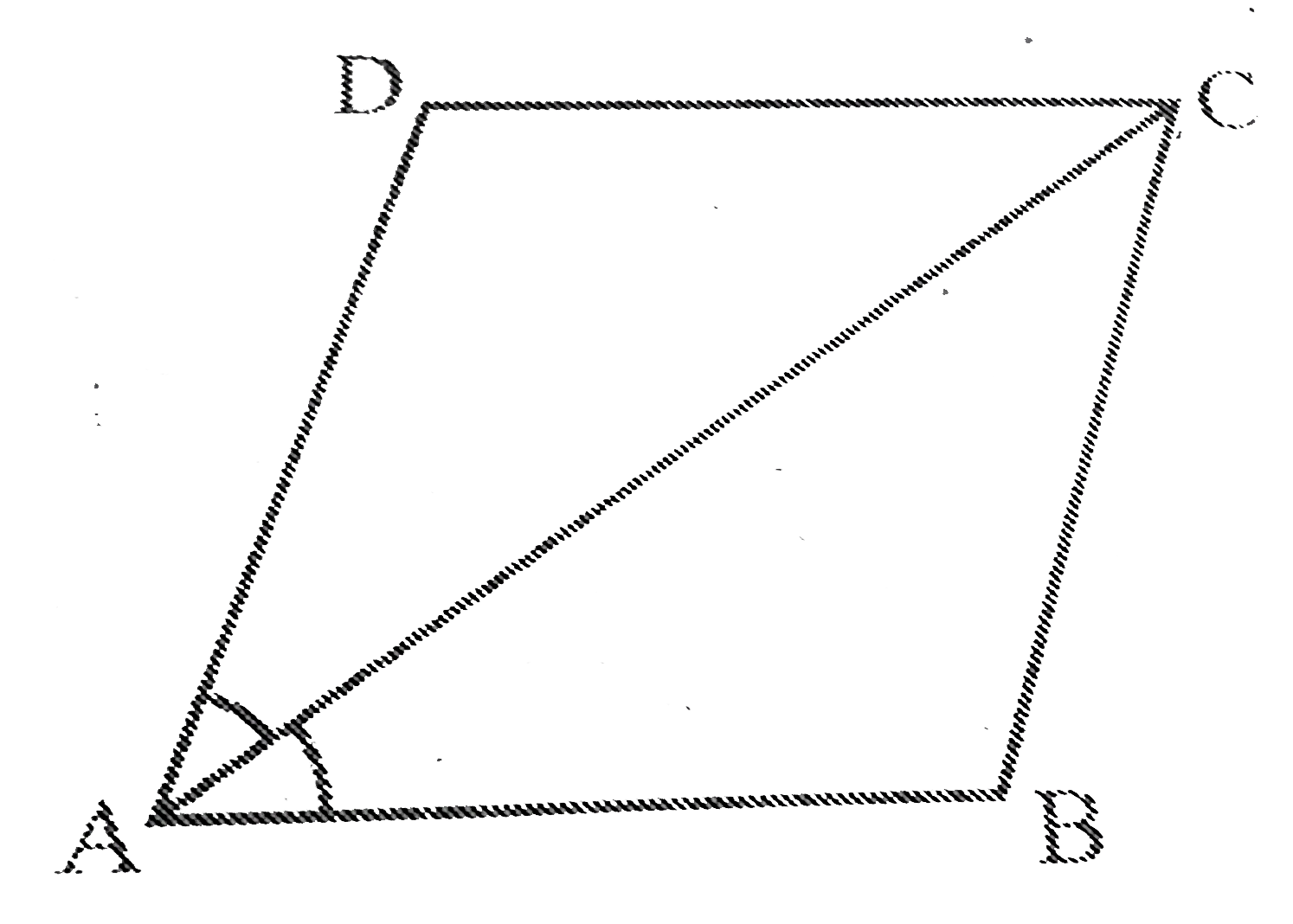
ii) From Equation (4), we obtain


`∠DAC = ∠DCA`


`DA = DC` (Side opposite to equal angles are equal)


However, `DA = BC` and `AB = CD` (Opposite sides of a parallelogram are equal)


Thus, `AB = BC = CD = DA`

Hence, ABCD is a rhombus.