Question

Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus

Explanation

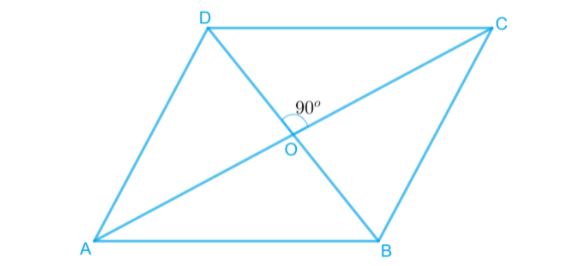
Given: The diagonals of a quadrilateral bisect each other at right angles.


To show that a given quadrilateral is a rhombus, we have to show it is a parallelogram and all the sides are equal.


Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus


Let `ABCD` be a quadrilateral, whose diagonals `AC` and `BD` bisect each other at the right angle.


So, we have, `OA = OC, OB = OD`, and `∠AOB = ∠BOC = ∠COD = ∠AOD = 90^@`.


To prove ABCD a rhombus, we have to prove ABCD is a parallelogram and all the sides of ABCD are equal.


In `ΔAOD` and `ΔCOD`,


`OA = OC` (Diagonals bisect each other)


`∠AOD = ∠COD = 90^@` (Given)


`OD = OD` (Common)


`∴ ΔAOD ≅ ΔCOD` (By SAS congruence rule)


`∴ AD = CD` (By CPCT) ...............(1)


Similarly, it can be proved that


`AD = AB` and `CD = BC` .................(2)


From Equations (1) and (2), `AB = BC = CD = AD`


Since opposite sides of quadrilateral ABCD are equal, it can be said that ABCD is a parallelogram. Since all sides of a parallelogram ABCD are equal, it can be said that ABCD is a rhombus.