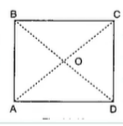
Show that the diagonals of a square are equal and bisect each other at right angles.
To show that the diagonals of a square are equal and bisect each other at right angles, we can follow these steps:
1. Define the Square: Let the square be represented as ABCD, where A, B, C, and D are the vertices of the square.
2. Identify the Diagonals: The diagonals of the square are AC and BD.
3. Congruent Triangles: To prove that the diagonals are equal, we will consider the triangles formed by the diagonals. We will analyze triangles ABD and ACD.
4. Common Side: In triangles ABD and ACD, the side AD is common to both triangles.
5. Equal Sides: Since ABCD is a square, we know that AB = AD and AC = CD (all sides of a square are equal).
6. Right Angles: The angle at vertex A (∠BAD) is 90 degrees because all angles in a square are right angles.
7. Apply SAS Congruence: We have:
- Side AD is common.
- AB = CD (equal sides of the square).
- ∠BAD = ∠CAD = 90 degrees (right angles).
By the Side-Angle-Side (SAS) congruence criterion, triangles ABD and ACD are congruent.
8. Conclusion from Congruence: Since triangles ABD and ACD are congruent, their corresponding parts are equal. Therefore, we have:
- AC = BD (the diagonals are equal).
9. Bisecting Each Other: Since ABCD is a square, it is also a parallelogram. In a parallelogram, the diagonals bisect each other. Thus, the diagonals AC and BD bisect each other at point O (the intersection point of the diagonals).
10. Right Angles at Intersection: Now, to show that the diagonals bisect each other at right angles, we will consider triangles AOB and COB.
11. Common Side and Equal Sides: In triangles AOB and COB:
- OB is common.
- AO = OC (since diagonals bisect each other).
- AB = CB (sides of the square are equal).
12. Apply SSS Congruence: By the Side-Side-Side (SSS) congruence criterion, triangles AOB and COB are congruent.
13. Conclusion from Congruence: Since triangles AOB and COB are congruent, we have:
- ∠AOB = ∠COB.
14. Linear Pair of Angles: Since ∠AOB and ∠COB are linear pairs, we know that:
- ∠AOB + ∠COB = 180 degrees.
- If ∠AOB = ∠COB, then 2∠AOB = 180 degrees, which implies ∠AOB = 90 degrees.
15. Final Conclusion: Therefore, the diagonals AC and BD not only are equal but also bisect each other at right angles.
- Side AD is common.
- AB = CD (equal sides of the square).
- ∠BAD = ∠CAD = 90 degrees (right angles).
By the Side-Angle-Side (SAS) congruence criterion, triangles ABD and ACD are congruent.
- AC = BD (the diagonals are equal).
- OB is common.
- AO = OC (since diagonals bisect each other).
- AB = CB (sides of the square are equal).
- ∠AOB = ∠COB.
- ∠AOB + ∠COB = 180 degrees.
- If ∠AOB = ∠COB, then 2∠AOB = 180 degrees, which implies ∠AOB = 90 degrees.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If the diagonals of a quadrilateral are equal and bisect each other at right angles, then the quadrilateral is a
AreactangleBsquareCrhombusDtrapezium - Question 2 - Select One
Prove that; If the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
ArhombusBtrapeziumCrectangleDkite
The diagonals of a rhombus are unequal and bisect each other at right angle
View SolutionThe diagonals of a rectangle are equal and bisect each other
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionThe diagonals of a square are equal and perpendicular to each other.
View Solution