Show that the diagonals of a square are equal and bisect each other at right angles.
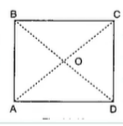
To prove that the diagonals of a square are equal and bisect each other at right angles, we will follow a systematic approach. Let's denote the square as ABCD, where A, B, C, and D are the vertices of the square. The diagonals are AC and BD, and they intersect at point O.
Step 1: Prove that the diagonals are equal.
1. Identify the triangles: Consider triangles AOD and BOC.
2. Sides of the square: Since ABCD is a square, all sides are equal. Thus, AD = BC.
3. Common side: The diagonal DC is common to both triangles AOD and BOC.
4. Angles: The angles at A and B are both right angles (90 degrees) because the angles in a square are right angles.
5. Congruence: By the Side-Angle-Side (SAS) criterion, triangles AOD and BOC are congruent.
6. Conclusion: Therefore, AC = BD by Corresponding Parts of Congruent Triangles (CPCT).
Step 2: Prove that the diagonals bisect each other.
1. Identify the triangles: Now, consider triangles AOB and COD.
2. Sides of the square: Since AD = BC, and AO = OC (as we will prove), we have two equal sides.
3. Common side: The diagonal AC is common to both triangles AOB and COD.
4. Congruence: By the Side-Side-Side (SSS) criterion, triangles AOB and COD are congruent.
5. Conclusion: Therefore, AO = OC and BO = OD by CPCT.
Step 3: Prove that the diagonals bisect each other at right angles.
1. Identify the triangles: Now, consider triangles AOD and BOC again.
2. Congruence: We already established that triangles AOD and BOC are congruent.
3. Angles: Since the triangles are congruent, the angles at O (angle AOB and angle COD) are equal.
4. Sum of angles: The sum of angles around point O is 360 degrees. Since AOB and COD are equal, we can denote them as x.
5. Equation: Thus, 2x + 2x = 360 degrees, leading to x = 90 degrees.
6. Conclusion: Therefore, the diagonals bisect each other at right angles.
Final Conclusion:
We have shown that the diagonals of the square are equal (AC = BD), bisect each other (AO = OC and BO = OD), and intersect at right angles (90 degrees).
1. Identify the triangles: Consider triangles AOD and BOC.
2. Sides of the square: Since ABCD is a square, all sides are equal. Thus, AD = BC.
3. Common side: The diagonal DC is common to both triangles AOD and BOC.
4. Angles: The angles at A and B are both right angles (90 degrees) because the angles in a square are right angles.
5. Congruence: By the Side-Angle-Side (SAS) criterion, triangles AOD and BOC are congruent.
6. Conclusion: Therefore, AC = BD by Corresponding Parts of Congruent Triangles (CPCT).
1. Identify the triangles: Now, consider triangles AOB and COD.
2. Sides of the square: Since AD = BC, and AO = OC (as we will prove), we have two equal sides.
3. Common side: The diagonal AC is common to both triangles AOB and COD.
4. Congruence: By the Side-Side-Side (SSS) criterion, triangles AOB and COD are congruent.
5. Conclusion: Therefore, AO = OC and BO = OD by CPCT.
1. Identify the triangles: Now, consider triangles AOD and BOC again.
2. Congruence: We already established that triangles AOD and BOC are congruent.
3. Angles: Since the triangles are congruent, the angles at O (angle AOB and angle COD) are equal.
4. Sum of angles: The sum of angles around point O is 360 degrees. Since AOB and COD are equal, we can denote them as x.
5. Equation: Thus, 2x + 2x = 360 degrees, leading to x = 90 degrees.
6. Conclusion: Therefore, the diagonals bisect each other at right angles.
We have shown that the diagonals of the square are equal (AC = BD), bisect each other (AO = OC and BO = OD), and intersect at right angles (90 degrees).
Topper's Solved these Questions
- QUADRILATERALSBook:NCERTChapter:QUADRILATERALSExercise:SOLVED EXAMPLES
Explore 8 Videos
- QUADRILATERALSBook:NCERTChapter:QUADRILATERALSExercise:SOLVED EXAMPLES
Explore 8 Videos
- PROBABILITYBook:NCERTChapter:PROBABILITYExercise:SOLVED EXAMPLES
Explore 10 Videos
- STATISTICSBook:NCERTChapter:STATISTICSExercise:EXERCISE 14.1
Explore 2 Videos
Similar Questions
Knowledge Check
If the diagonals of a quadrilateral are equal and bisect each other at right angles, then the quadrilateral is a
AreactangleBsquareCrhombusDtrapeziumProve that; If the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
ArhombusBtrapeziumCrectangleDkite
In figure, Show that if the diagonals of a quadrilateral are equal and bisect each other at right angle, then it is a square.
View SolutionThe diagonals of a rectangle are equal and bisect each other
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionProve that; If the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View Solution