ABCD is a quadrilateral in which diagonal BD = 64 cm. AL⊥BD and CM⊥BD, such that AL=13.2cm and CM=16.8cm. The area of the quadrilateral ABCD is square centimeters is :
a) 422.4
b) 690.0
c) 537.6
d) 960.0
The correct Answer is:D
To find the area of quadrilateral ABCD, we can break it down into two triangles: triangle ABD and triangle BCD. The area of a triangle can be calculated using the formula:
Area=12×base×height
1. Identify the Given Values:
- Diagonal BD=64cm
- Height from point A to line BD (denoted as AL) = 13.2cm
- Height from point C to line BD (denoted as CM) = 16.8cm
2. Calculate the Area of Triangle ABD:
- For triangle ABD, the base is BD and the height is AL.
- Using the area formula:
Area of △ABD=12×BD×AL=12×64×13.2
3. Calculate the Area of Triangle BCD:
- For triangle BCD, the base is also BD and the height is CM.
- Using the area formula:
Area of △BCD=12×BD×CM=12×64×16.8
4. Sum the Areas of Both Triangles:
- The total area of quadrilateral ABCD is the sum of the areas of triangles ABD and BCD:
Area of ABCD=Area of △ABD+Area of △BCD
5. Substituting the Values:
- Calculate the area of triangle ABD:
Area of △ABD=12×64×13.2=32×13.2=422.4cm2
- Calculate the area of triangle BCD:
Area of △BCD=12×64×16.8=32×16.8=537.6cm2
6. Final Calculation:
- Now, sum the areas:
Area of ABCD=422.4+537.6=960cm2
Conclusion:
The area of quadrilateral ABCD is 960cm2.
- Diagonal BD=64cm
- Height from point A to line BD (denoted as AL) = 13.2cm
- Height from point C to line BD (denoted as CM) = 16.8cm
- For triangle ABD, the base is BD and the height is AL.
- Using the area formula:
Area of △ABD=12×BD×AL=12×64×13.2
- For triangle BCD, the base is also BD and the height is CM.
- Using the area formula:
Area of △BCD=12×BD×CM=12×64×16.8
- The total area of quadrilateral ABCD is the sum of the areas of triangles ABD and BCD:
Area of ABCD=Area of △ABD+Area of △BCD
- Calculate the area of triangle ABD:
Area of △ABD=12×64×13.2=32×13.2=422.4cm2
- Calculate the area of triangle BCD:
Area of △BCD=12×64×16.8=32×16.8=537.6cm2
- Now, sum the areas:
Area of ABCD=422.4+537.6=960cm2
The area of quadrilateral ABCD is 960cm2.
Topper's Solved these Questions
- QUADRILATERALBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:QUADRILATERALExercise:EXERCISE
Explore 48 Videos
- PROFIT & LOSSBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:PROFIT & LOSSExercise:Questions
Explore 200 Videos
- RATIO & PROPORTIONBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:RATIO & PROPORTIONExercise:QUESTIONS
Explore 113 Videos
Similar Questions
In the given figure ABCD is a quadrilateral in which diagonal BD=24cm,AL⊥BDandCM⊥BD such that AL=9cm and CM=12 cm. Calculate the area of the quadrilateral .
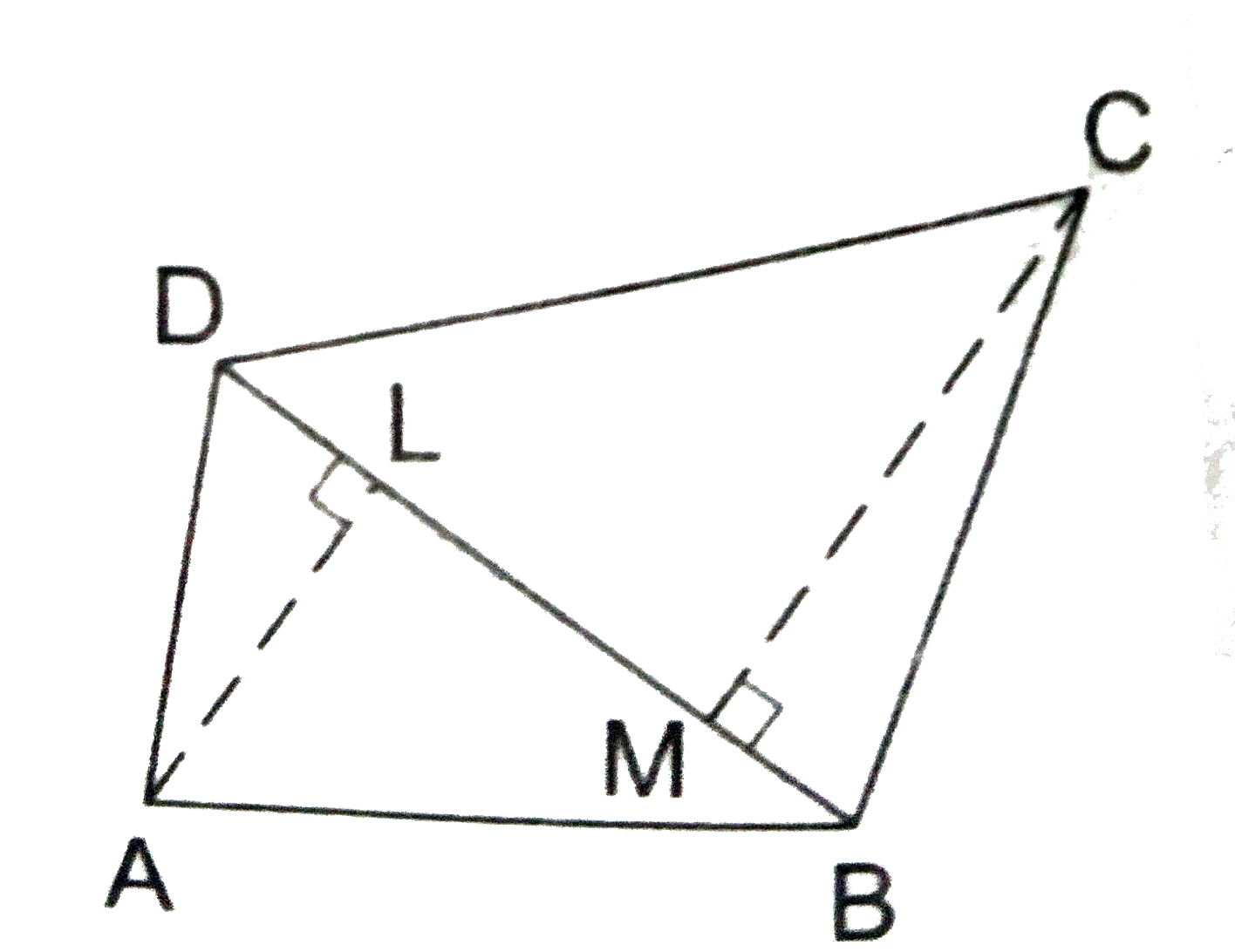
View SolutionFind the area of quadrilateral ABCD in which diagonal BD = 24 cm. AL⊥BD and CM⊥BD.such that AL = 5 cm and CM = 8 cm.
View Solution
Knowledge Check
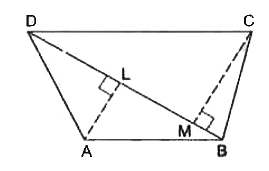
In the adjoining figure, ABCD is a quadrilateral in which diag. BD = 14 cm. If AL⊥BDandCM⊥BD such that AL = 8 cm and CM = 6 cm, find the area of quad. ABCD.
 A96cm2B95cm2C98cm2D97cm2
A96cm2B95cm2C98cm2D97cm2In a quadrilateral ABCD, it is given that BD = 16 cm. If AL⊥BD and CM⊥BD such that AL = 9 cm and CM = 7 cm, then ar( quad. ABCD) is
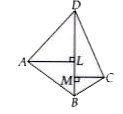 A256 cm2B128 cm2C64 cm2D96 cm2
A256 cm2B128 cm2C64 cm2D96 cm2In the figure, ABCD is a quadrilateral BD = 20 cm. If AL⊥BD and CM⊥BD such that AL = 10 cm and CM = 5 cm, find the area of quad. ABCD.
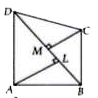 A150 cm2B180 cm2C100 cm2D140 cm2
A150 cm2B180 cm2C100 cm2D140 cm2
In the given figure, ABCD is a quadrillateral in which BD=14cm,AL⊥BD,CM⊥BD such that AL = 6 cm and CM = 8 cm. Find the area of aquad. ABCD.
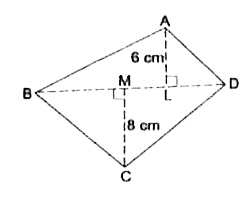
View SolutionIn the given figure, ABCD is a quadrilateral - shaped field in which diagonal BD is 36 m, AL⊥BD and CM⊥BD such that AL = 19 m and CM = 11 m. Find the area of the field.

View SolutionIf ABCD is a quadrilateral whose diagonals AC and BD intersect at O, then

View SolutionIn a quadrilateral ABCD, it is given that BD = 16 cm. If AL⊥BDandCM⊥BD such that AL = 9 cm and CM = 7 cm then ar(quad. ABCD) = ?
View SolutionIn a quadrilateral ABCD, it is given that BD = 16 cm. If AL perpendicular BD and CM perpendicular BD such that AL = 9 cm and CM = 7 cm, then area (quadrilateral ABCD) is equal to
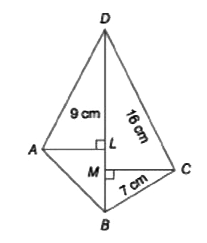
View Solution

