ABCD is a cyclic quadrilateral. The tangent at A and C meet at a point P. If then will be euqal to :
The correct Answer is:B
To solve the problem, we need to use the properties of cyclic quadrilaterals and the angles formed by tangents.
1. Understanding the Problem: We have a cyclic quadrilateral ABCD, and the tangents at points A and C meet at point P. We are given that angle ABC = 100° and need to find angle APC.
2. Using the Tangent Property: The tangent to a circle at any point is perpendicular to the radius drawn to the point of tangency. Therefore, the angle between the tangent at point A and the line segment AP (which is a radius to point A) is 90°.
3. Identifying Angles: Since angle ABC is given as 100°, we can find angle BAP, which is the angle between line AB and the tangent at A. By the property of tangents, angle BAP = 90° - angle ABC = 90° - 100° = -10°. This indicates that we need to reconsider our approach since angles cannot be negative.
4. Using Cyclic Quadrilateral Properties: In a cyclic quadrilateral, opposite angles are supplementary. Therefore, angle ABC + angle ADC = 180°. Since angle ABC = 100°, angle ADC = 180° - 100° = 80°.
5. Finding Angle APC: Now, we can use the fact that angle APC is equal to the sum of angles BAP and CAD. Since angle BAP is 90° (from the tangent property) and angle CAD is equal to angle ADC (which is 80°), we have:
angle APC=angle BAP+angle CAD=90°+80°=170°.
Final Answer:
Thus, angle APC = 170°.
angle APC=angle BAP+angle CAD=90°+80°=170°.
Thus, angle APC = 170°.
Topper's Solved these Questions
- QUADRILATERALBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:QUADRILATERALExercise:EXERCISE
Explore 48 Videos
- PROFIT & LOSSBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:PROFIT & LOSSExercise:Questions
Explore 200 Videos
- RATIO & PROPORTIONBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:RATIO & PROPORTIONExercise:QUESTIONS
Explore 113 Videos
Similar Questions
Knowledge Check
ABCD is a cyclic quadrilateral. Diagonals AC and BD meets at P. If ∠APB=110∘ and ∠CBD=30∘, then ∠ADB measures
A55∘B30∘C70∘D80∘If ABCD is a cyclic quadrilateral, then cosA+cosB is equal to
A0BcosC+cosDC−(cosC+cosD)DcosC−cosDIn the given figure, ABCD is a cyclic quadrilateral and diagonals D bisect each other at P. If ∠DBC=60∘and∠BAC=30∘, then ∠BCD is:
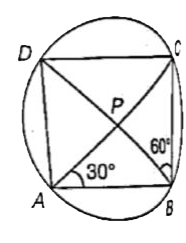 A90∘B60∘C80∘Dnone of the above
A90∘B60∘C80∘Dnone of the above
In Figure, ABCD is a cyclic quadrilateral. Find the value of x
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
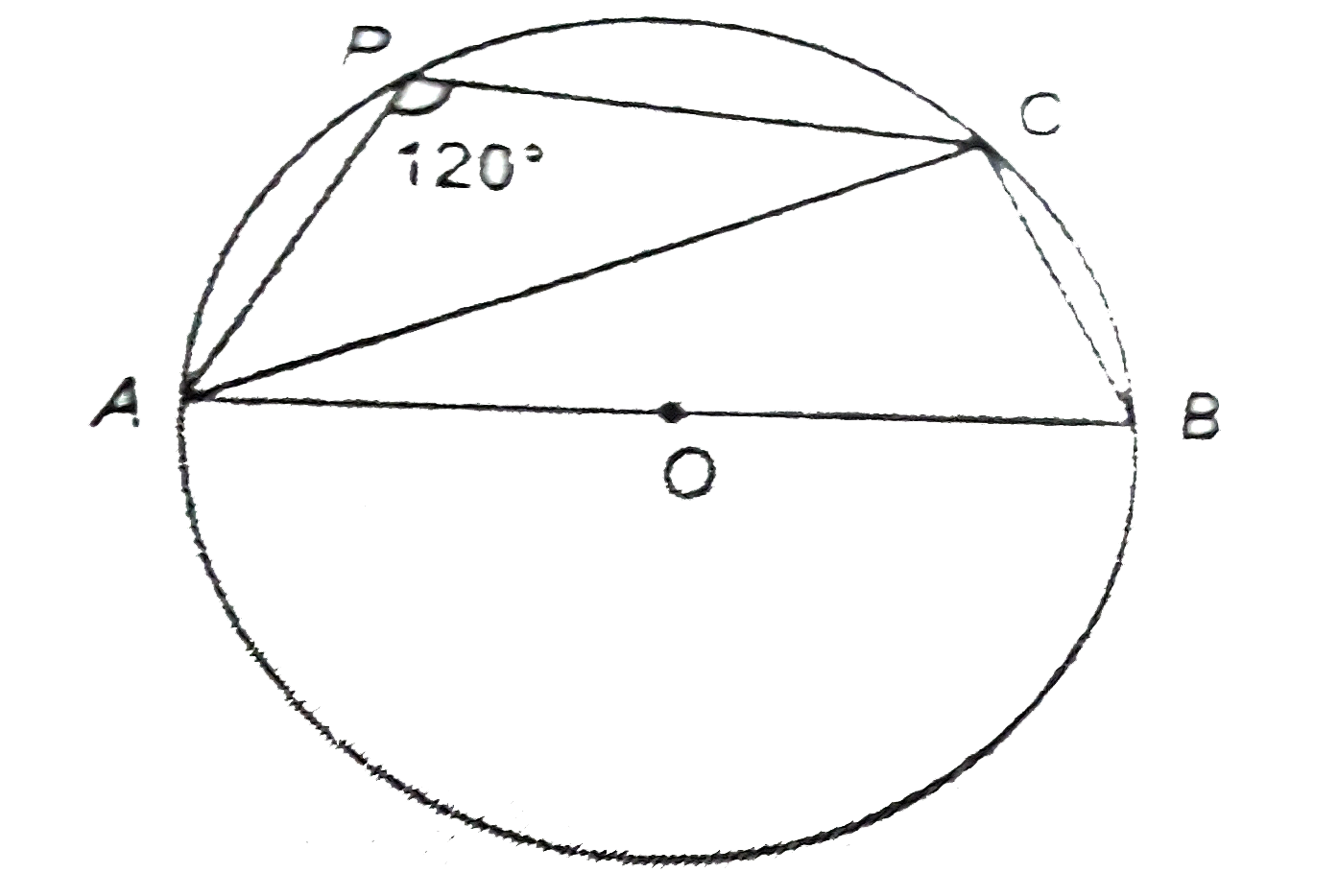
View SolutionABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ=65∘, then ∠BCD is:
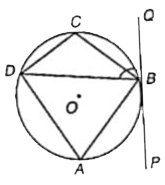
View SolutionABCD is a cyclic quadrilateral in which AB is a diameter , ,BC=CDand∠ABD=50∘ then ∠DBC is :
View SolutionABCD is a cyclic quadrilateral. AB and DC are produced to meet at P. If ∠ADC=70degreeand∠DAB=60degree, then the ∠PBC+∠PCB is
View Solution
