In a quadrilateral ABCD, OA and OB are the angle bisectors of ∠DAB and ∠CBA. If ∠ADC=70∘ and ∠BCD=80∘ then find ∠AOB ?
70∘
80∘
90∘
75∘
The correct Answer is:D
To find the angle ∠AOB in the quadrilateral ABCD where OA and OB are the angle bisectors of ∠DAB and ∠CBA respectively, we can follow these steps:
Step 1: Understand the angles in the quadrilateral
In any quadrilateral, the sum of the interior angles is 360∘. We know:
- ∠ADC=70∘
- ∠BCD=80∘
Step 2: Calculate the sum of the remaining angles
Let ∠DAB=x and ∠CBA=y. According to the properties of quadrilaterals, we have:
x+y+70∘+80∘=360∘
This simplifies to:
x+y+150∘=360∘
Thus,
x+y=360∘−150∘=210∘
Step 3: Use the angle bisector property
Since OA and OB are the angle bisectors, we have:
∠DAB=xand∠CBA=y
The angle bisectors divide these angles into two equal parts:
∠OAD=x2and∠OBA=y2
Step 4: Relate the angles to triangle AOB
In triangle AOB, we know that:
∠AOB+∠OAD+∠OBA=180∘
Substituting the values:
∠AOB+x2+y2=180∘
Since x+y=210∘, we can substitute:
∠AOB+210∘2=180∘
This simplifies to:
∠AOB+105∘=180∘
Thus,
∠AOB=180∘−105∘=75∘
Final Answer
Therefore, the angle ∠AOB is 75∘.
---
In any quadrilateral, the sum of the interior angles is 360∘. We know:
- ∠ADC=70∘
- ∠BCD=80∘
Let ∠DAB=x and ∠CBA=y. According to the properties of quadrilaterals, we have:
x+y+70∘+80∘=360∘
This simplifies to:
x+y+150∘=360∘
Thus,
x+y=360∘−150∘=210∘
Since OA and OB are the angle bisectors, we have:
∠DAB=xand∠CBA=y
The angle bisectors divide these angles into two equal parts:
∠OAD=x2and∠OBA=y2
In triangle AOB, we know that:
∠AOB+∠OAD+∠OBA=180∘
Substituting the values:
∠AOB+x2+y2=180∘
Since x+y=210∘, we can substitute:
∠AOB+210∘2=180∘
This simplifies to:
∠AOB+105∘=180∘
Thus,
∠AOB=180∘−105∘=75∘
Therefore, the angle ∠AOB is 75∘.
Topper's Solved these Questions
- QUADRILATERALBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:QUADRILATERALExercise:EXERCISE
Explore 48 Videos
- PROFIT & LOSSBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:PROFIT & LOSSExercise:Questions
Explore 200 Videos
- RATIO & PROPORTIONBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:RATIO & PROPORTIONExercise:QUESTIONS
Explore 113 Videos
Similar Questions
Knowledge Check
In a quadrilateral ABCD, OA and OB are the angle bi- sectors of ∠DABand∠CBA. If∠ADC=70 and ∠ BCD= 80 then find the angle AOB
A70∘B80∘C90∘D75∘In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively, ∠C=70∘and∠D=30∘. Then, ∠AOB=?
A50∘B130∘C80∘D100∘
In a quadrilateral ABCD, E is a point in the interior of the quadrilateral such that DE and CE are the bisector of ∠D and ∠C, respectively, If ∠B=82∘ and ∠DEC=80∘ then ∠A= ?
एक चतुर्भुज ABCD में, E, चतुर्भुज के भीतरी भाग का एक बिंदु इस प्रकार है की DE और CE क्रमश ∠D और ∠C, के द्विभाजक हैं, यदि ∠B=82∘और ∠DEC=80∘ तो ∠A = ?
View SolutionIn a quadrilateral ABCD, the bisectors of ∠C and ∠D meet at E. If ∠CED=56∘ and ∠A=49∘, then the measure of ∠B is:
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect each other at point O. If ∠CAB=25∘ and ∠BCD=85∘ then find ∠CBD.
View SolutionIn Fig , ABCD is a cyclic quadrilateral . If ∠BAC=50∘and∠DBC=60∘ then find ∠BCD.
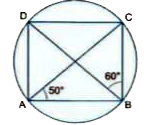
View Solution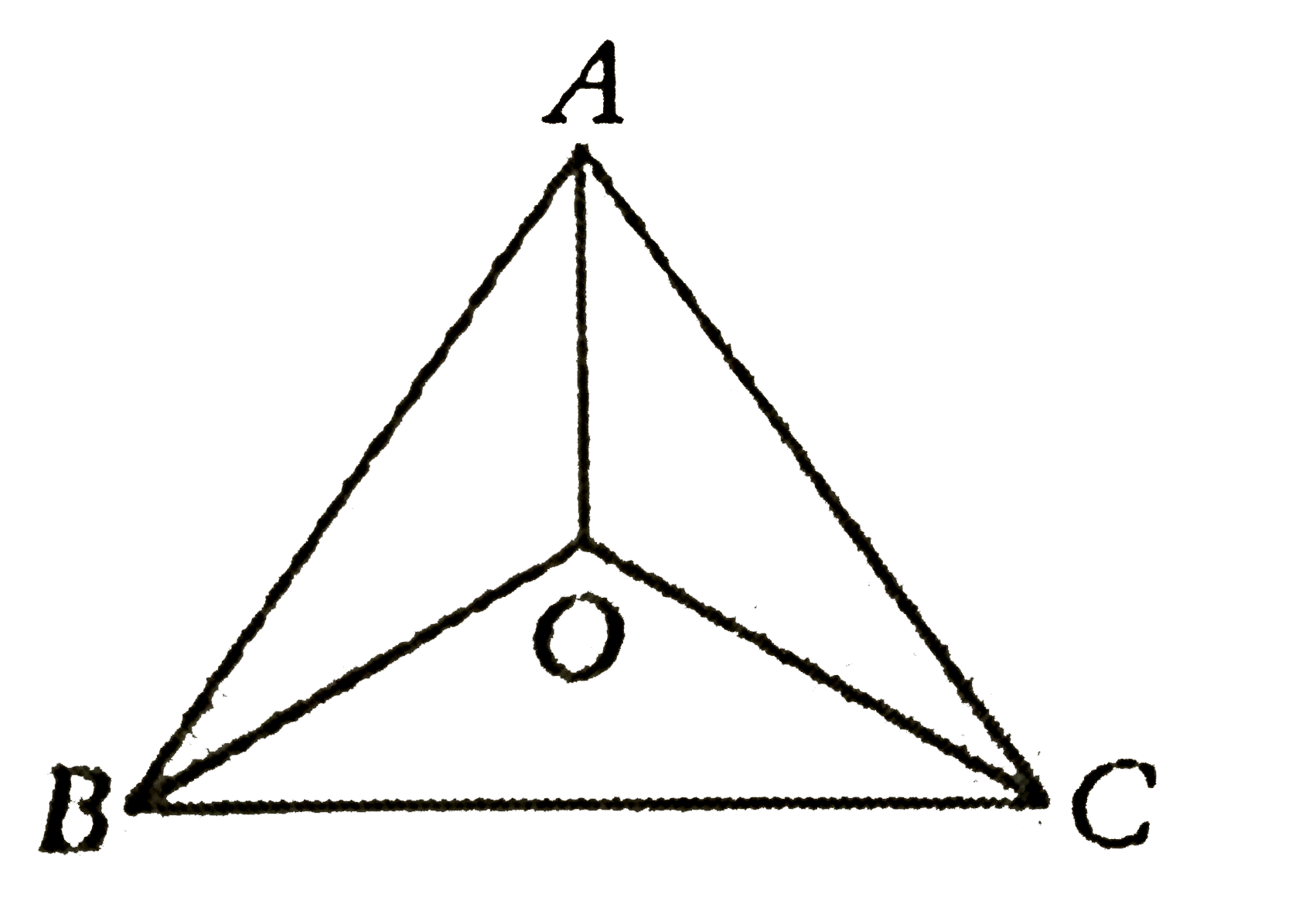
In the above ΔABC ( not to scale ), OA is the angle bisector of ∠BAC . If OB=OC,∠OAC=40∘ and ∠ABO=20∘. If ∠OCB=12∠ACO, then find ∠BOC.
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral. If ∠DBC=60∘ and ∠BAC=40∘ , then find the value of ∠BCD .
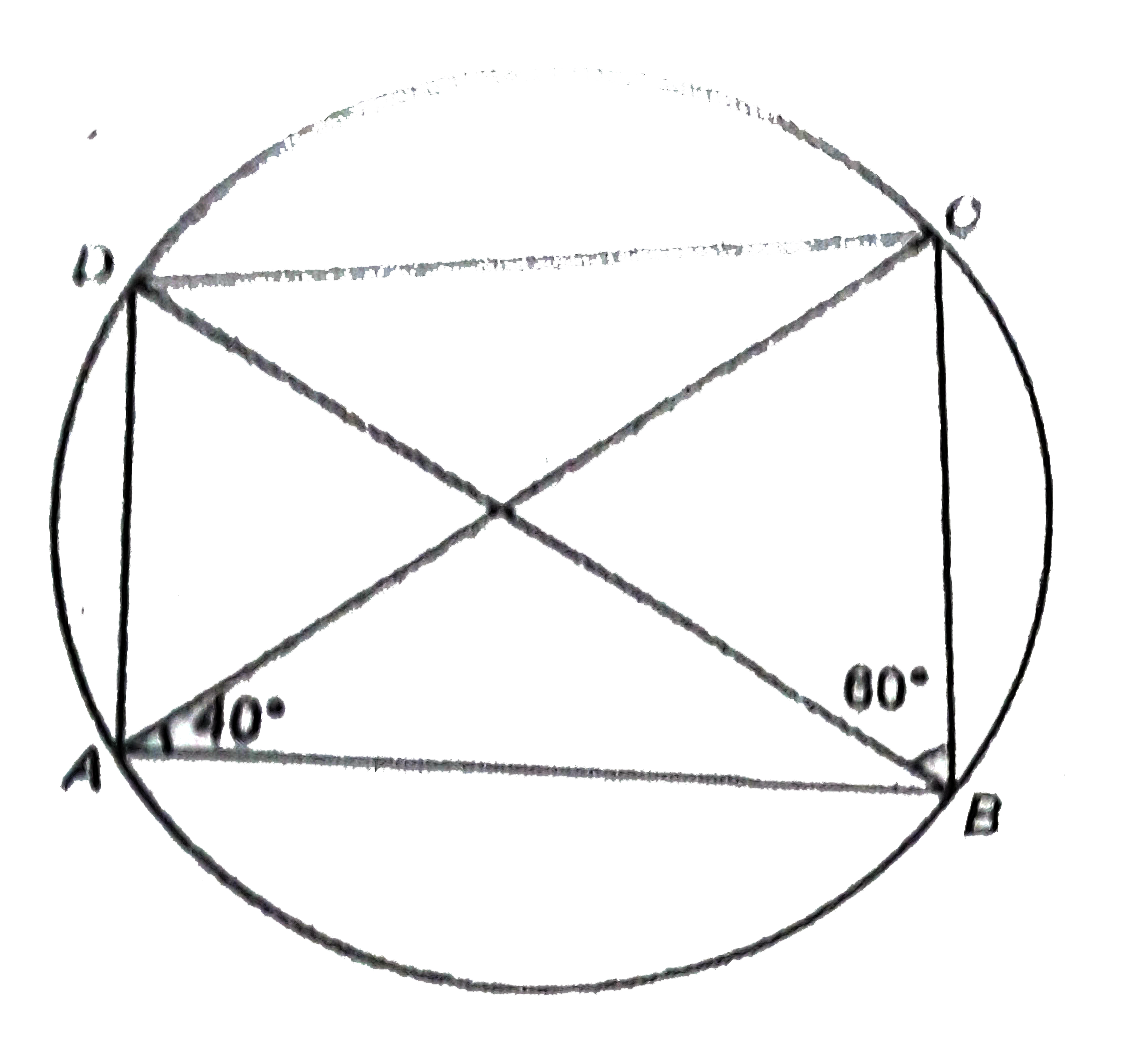
View Solution
