ABCD is a cyclic trapezium whose side AD and BC are parallel to each other. If ∠ABC=62∘ then the measure of the ∠BCD is :
120∘
118∘
62∘
28∘
The correct Answer is:C
To solve the problem, we need to find the measure of angle BCD in the cyclic trapezium ABCD, where AD is parallel to BC and angle ABC is given as 62 degrees.
1. Understanding the Properties of a Cyclic Trapezium:
- In a cyclic trapezium, the sum of the opposite angles is 180 degrees.
- Since AD is parallel to BC, we can use the properties of parallel lines and transversals.
2. Identify the Given Angle:
- We are given that angle ABC = 62 degrees.
3. Finding Angle DAB:
- Since AD is parallel to BC, angle DAB (which is the angle adjacent to angle ABC) can be found using the property of angles on the same side of a transversal.
- Therefore, angle DAB = 180 degrees - angle ABC
- Angle DAB = 180 degrees - 62 degrees = 118 degrees.
4. Finding Angle BCD:
- Now, we need to find angle BCD. Since ABCD is a cyclic trapezium, the opposite angles DAB and BCD must also sum to 180 degrees.
- Therefore, angle BCD = 180 degrees - angle DAB
- Angle BCD = 180 degrees - 118 degrees = 62 degrees.
5. Final Answer:
- The measure of angle BCD is 62 degrees.
Summary:
- Angle ABC = 62 degrees
- Angle DAB = 118 degrees
- Angle BCD = 62 degrees
- In a cyclic trapezium, the sum of the opposite angles is 180 degrees.
- Since AD is parallel to BC, we can use the properties of parallel lines and transversals.
- We are given that angle ABC = 62 degrees.
- Since AD is parallel to BC, angle DAB (which is the angle adjacent to angle ABC) can be found using the property of angles on the same side of a transversal.
- Therefore, angle DAB = 180 degrees - angle ABC
- Angle DAB = 180 degrees - 62 degrees = 118 degrees.
- Now, we need to find angle BCD. Since ABCD is a cyclic trapezium, the opposite angles DAB and BCD must also sum to 180 degrees.
- Therefore, angle BCD = 180 degrees - angle DAB
- Angle BCD = 180 degrees - 118 degrees = 62 degrees.
- The measure of angle BCD is 62 degrees.
- Angle ABC = 62 degrees
- Angle DAB = 118 degrees
- Angle BCD = 62 degrees
Topper's Solved these Questions
- QUADRILATERALBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - QUADRILATERALEXERCISE - EXERCISE
48 Videos
- PROFIT & LOSSBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PROFIT & LOSSEXERCISE - Questions
200 Videos
- RATIO & PROPORTIONBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - RATIO & PROPORTIONEXERCISE - QUESTIONS
113 Videos
Similar Questions
Knowledge Check
ABCD is a cyclic trapezium whose sides AD and BC are parallel to each other. If ∠ABC=72∘, then the measure of the ∠BCD is
A162∘B18∘C108∘D72∘ABCD is a cyclic trapezium whose sides AD and BC are parallel to each other. If ∠ABC=75∘ then the measure of ∠BCD is:
A75∘B95∘C45∘D105∘ABCD is a cyclic trapezium whose sides AD and BC are parallel to each other. If ∠ABC=72∘, then the measure of the ∠BCD is
A162∘B18∘C108∘D72∘
ABC is a triangle whose medians AD and BE are perpendicular to each other. If AD=p and BE=q then area of △ABC is
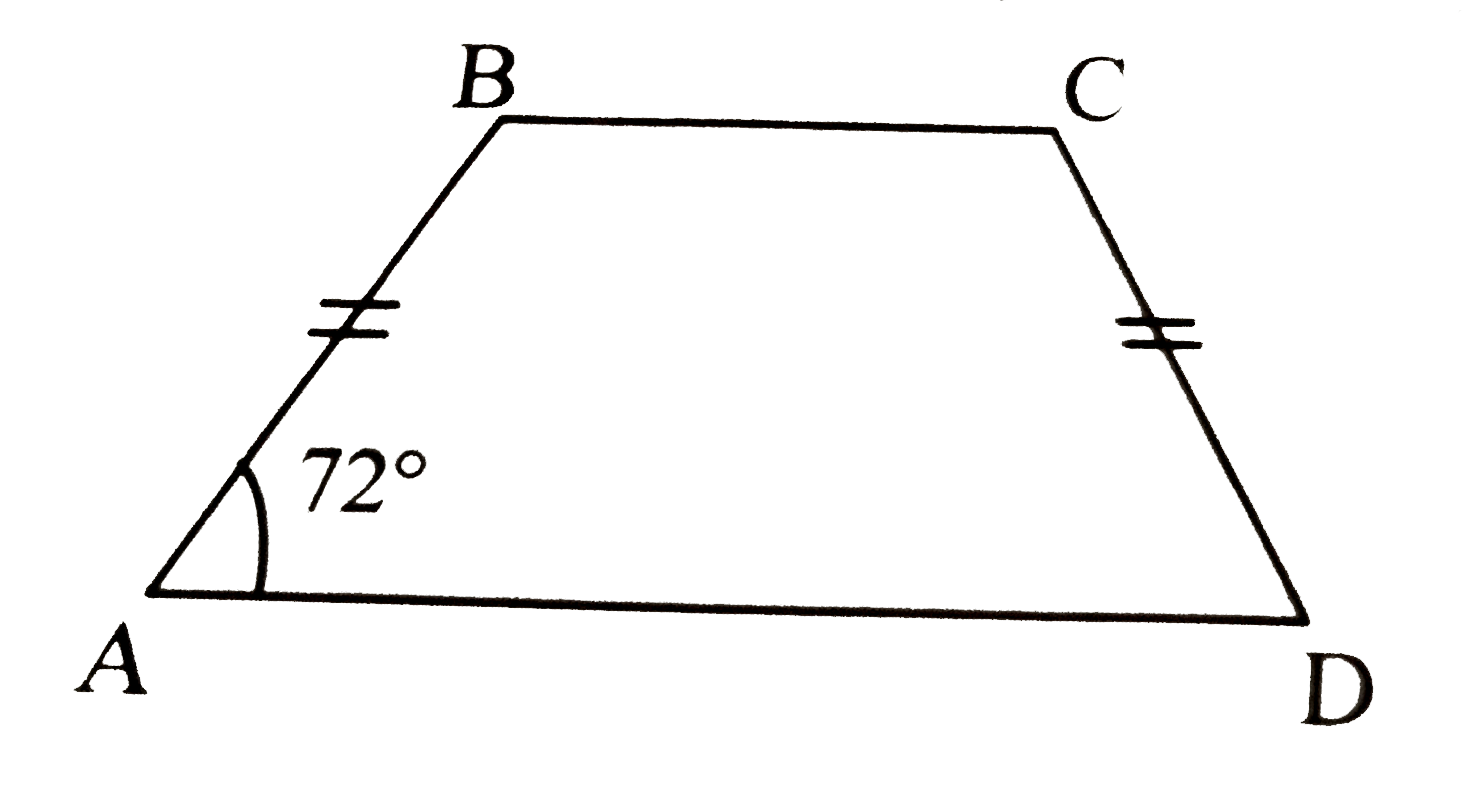
View SolutionIn trapezium ABCD, side BC ∣∣ side AD, side AB ≅ side DC. If ∠A=72∘ , then find the measures of ∠B and ∠D .
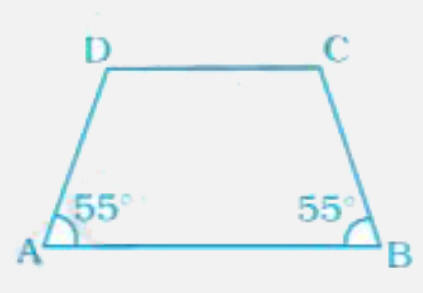
View SolutionIn the trapezium ABCD, the measure of∠D is
View SolutionABCD is a cyclic trapezium such that AD || BC. If ∠ABC=70∘, then the value of ∠BCD is :
View SolutionABCD is a cyclic trapezium with AD∣∣BC, If ∠A=105∘, then other three angles are
View Solution

