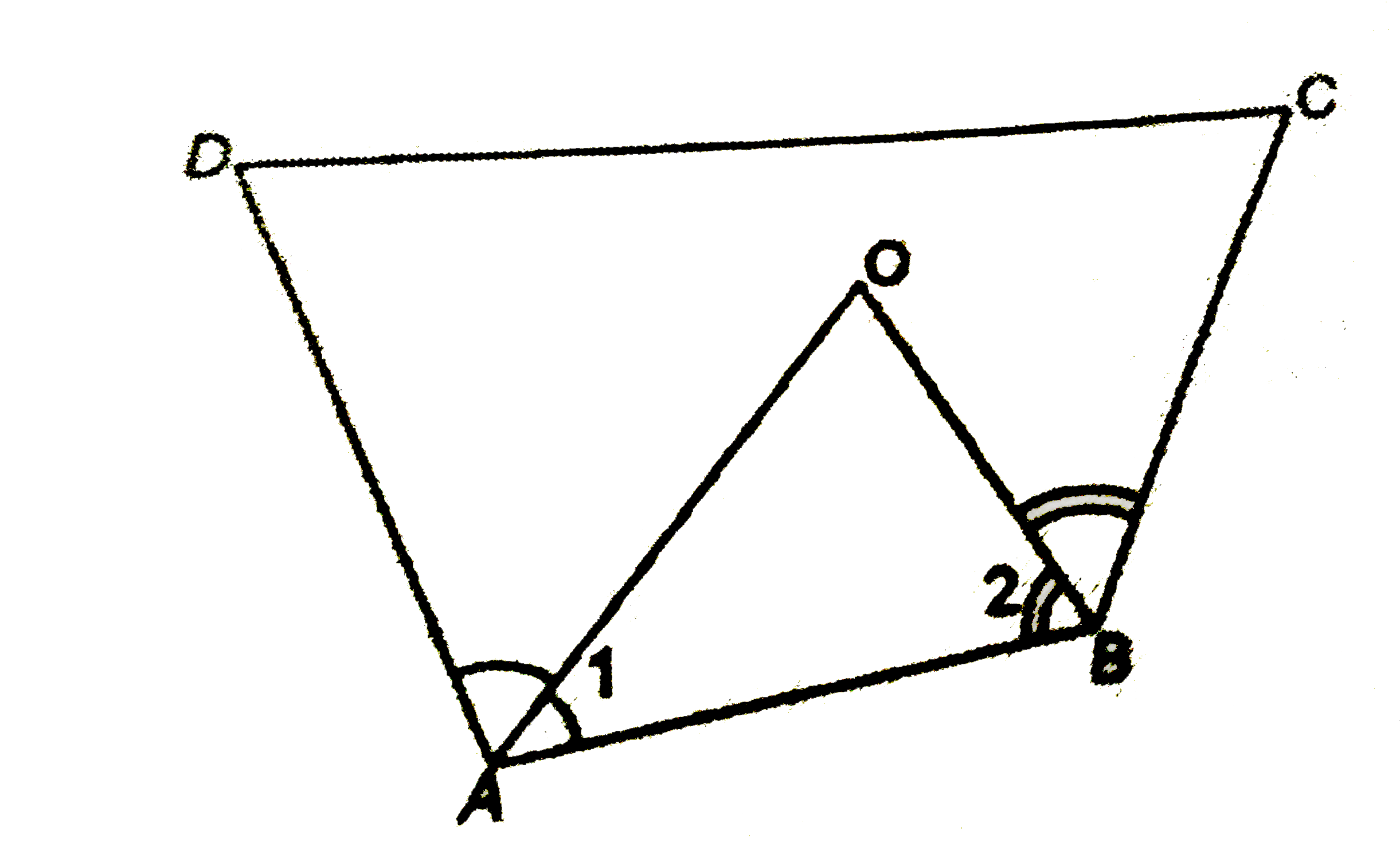
In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively. Prove that ∠AOB=12(∠C+∠D).
Video Solution
Text Solution
InΔΔOB+∠1+∠2=180∘
⇒ ∠AOB=180∘−(∠1+∠2)
⇒ ∠AOB=180∘−(∠A2+∠B2)
⇒ ∠AOB=180∘−12[360∘−(∠C+∠D)](∵∠A+∠B+∠C+∠D=360∘)
⇒ ∠AOB=180∘−180∘+12(∠C+∠D)
⇒ ∠AOB=12(∠C+∠D)
|
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHANChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHANChapter:STATISTICSExercise:Revision Exercise
Explore 10 Videos
Similar Questions
Knowledge Check
In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively, ∠C=70∘and∠D=30∘. Then, ∠AOB=?
A50∘B130∘C80∘D100∘In a quadrilateral ABCD, OA and OB are the angle bisectors of ∠DAB and ∠CBA. If ∠ADC=70∘ and ∠BCD=80∘ then find ∠AOB ?
A70∘B80∘C90∘D75∘In a triangle ABC , OB and OC are the bisector of angle ∠B and ∠C respectively . ∠BAC=60∘ . The angle ∠BOC will be :
A150∘B120∘C100∘D90∘
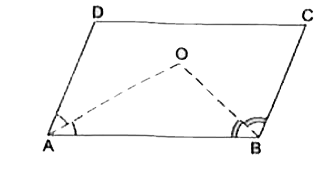
In the adjoining figure, ABCD is a parallelogram , AO and BO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB=90∘.
View SolutionIn a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B).
View SolutionIn a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B)
View SolutionIn the given figure, AB>AC. If BO and CO are the bisectors of ∠Band∠C respectively then
View SolutionIn a quadrilateral ABCD the linesegment bisecting ∠Cand∠D meet at E. Prove that ∠A+∠B=2∠CED.
View Solution

