In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B)
In quadrilateral ABCD,
CO and DO are the bisectors of ∠C and ∠D respectively.
In △COD,
∠DCO+∠CDO+∠COD=180∘ (sum of angles of a triangle)
1/2∠C+1/2∠D+∠COD=180∘
∠COD=180∘-1/2(∠C+∠D)
=180∘-1/2(∠C+∠D)
But∠A+∠B+∠C+∠D=360∘=∠C+∠D=360∘-(∠A+∠B)
Hence,∠COD=180∘-[360∘-∠A-∠B)
=180∘-180∘+1/2(∠A+∠B)
Hence Proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively, ∠C=70∘and∠D=30∘. Then, ∠AOB=?
A50∘B130∘C80∘D100∘
In a quadrilateral ABCD,AO andBO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionIn quadrilateral ABCD, AO and BO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionIn a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionIn a quadrilateral ABCD, cosAcosB+sinCsinD=
View SolutionIn the figure bisector of ∠B & ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
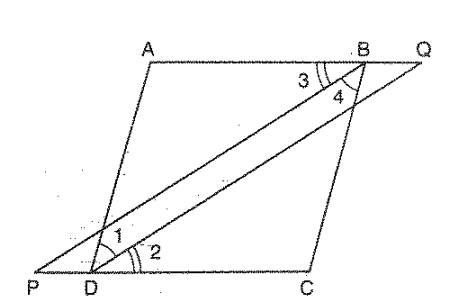
View SolutionIn the figure bisector of ∠B & ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that
∠P+∠Q=12(∠ABC+∠ADC).
View Solution
