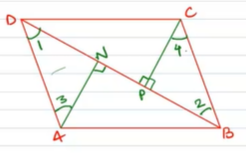
In Figure, and are perpendicular to the diagonal of a parallelogram Prove that :
(i)
(ii)
"(i)
in triangle ADN and CBP,
(since AD||CB and BD is a sector so alternate interior angles are equal)
so from AAS theorem ,
(ii)
from CPCT of above ,
Topper's Solved these Questions
Similar Questions
Knowledge Check
P and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Then which of the following is true?
ACQ is parallel to APBCQ is perpendicular to APCCQ intersects APDNone of these
P is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
View SolutionIn Figure, BM and DN are both perpendiculars to the segments AC and BM=DN . Prove that AC bisects BD
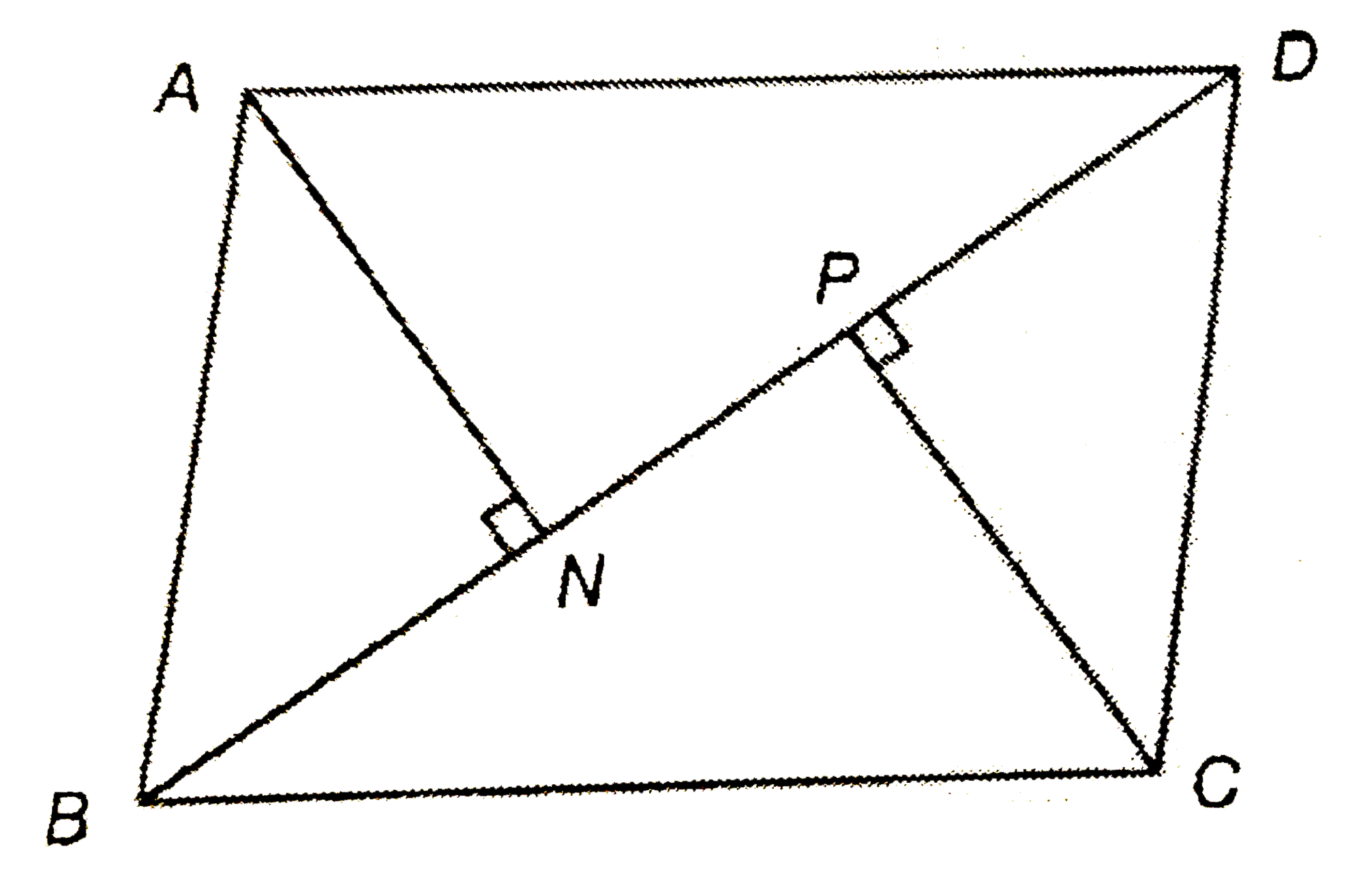
View SolutionIn the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
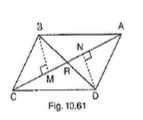
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
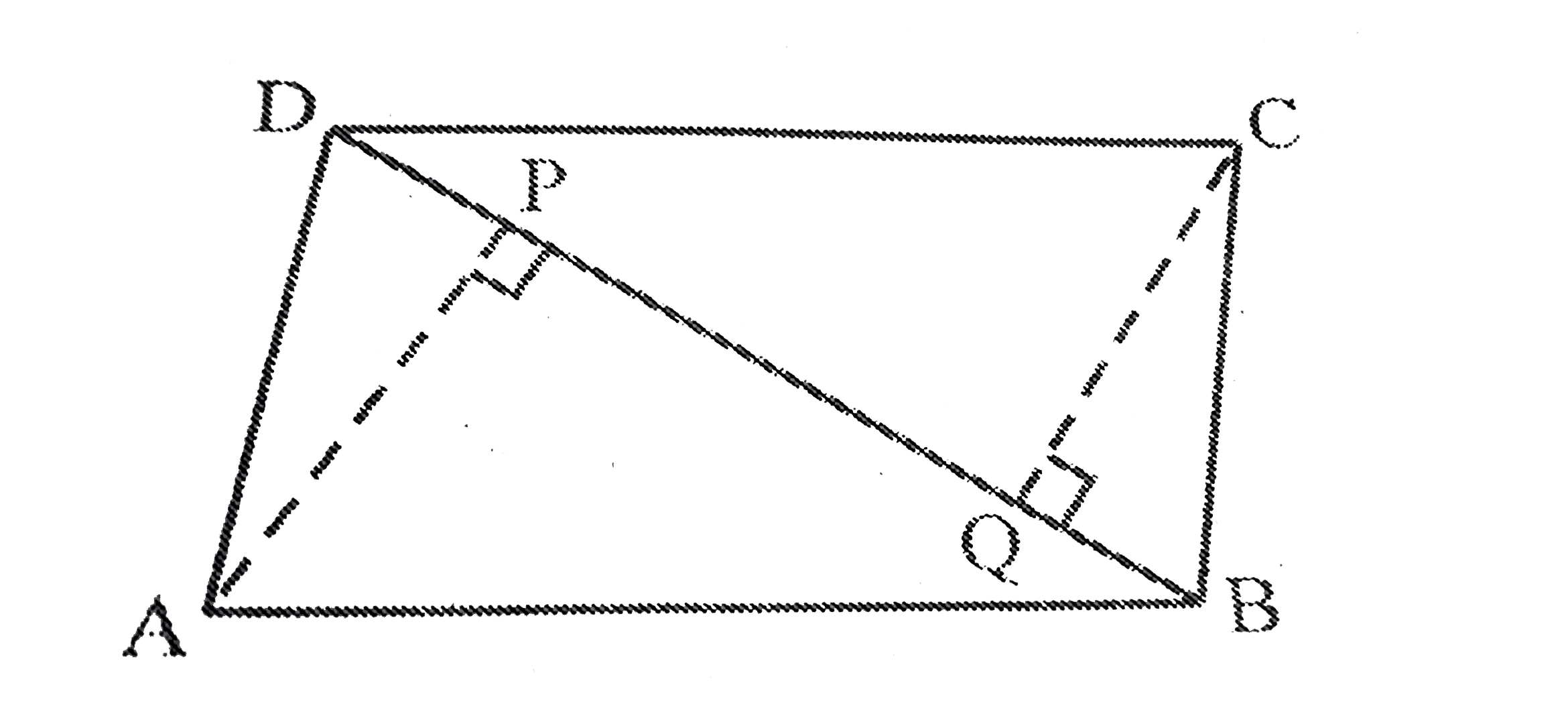
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) ΔAPB≅ ΔCQD
(ii) AP = CQ
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

View SolutionTwo points X and Y lie on the diagonal BD of a parallelogram ABCD such that DX = BT. Prove that □AXCY is a parallelogram.
View Solution