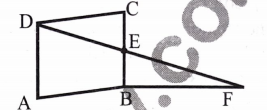
A B C D is a parallelogram and E is the mid-point of B C , DE and AB w

If in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
A $\frac{a}{4} - \frac{b}{4}$
B $\frac{a}{2} - \frac{b}{2}$
C $\frac{b}{4} - \frac{a}{4}$
D $\frac{b}{2} - \frac{a}{2}$
If a parallelogram ABCD, $| A B | = a, | A D | = b and | A C | = C,$ then DA. AB is equal to
A $\frac{1}{2} (a^{2} + b^{2} + c^{2})$
B $\frac{1}{2} (a^{2} - b^{2} + c^{2})$
C $\frac{1}{4} (a^{2} + b^{2} - c^{2})$
D $\frac{1}{3} (b^{2} + c^{2} - a^{2})$

$A B C D$ is a parallelogram and $E$ is the mid-point of $B C, D E and A B$ when produced meet at $F$ Then $A F =$
(a) $\frac{3}{2} A B$
(b) $2 A B$
(c) $3 A B$
(d) $\frac{5}{4} A B$