Two segments AC and BD bisect each other at O . Prove that ABCD is a parallelogram.
ABandCDbisect each other at O
AO=BOand CO=DO
in△COAand△DOB
GivenCO=OD,△COA=∠BOD(vertically opp angles)
AD=BD
△COA≅△BOD
(i)AC=BD(C.P.CT)
(ii)∠CAB=∠ABD(C.P.CT)
In △COBand △AOD
CO=OD(given)
BO=AO(given)
∠COB=∠AOD(vertically opp angles)
△COB≅△AOD(iii)
∠CBA=∠BAD(C.P. C.T)
AD∣∣CD(∠CBA=∠BAD)(which are altanate angles)
AD=CB(C.P.C.T)
Topper's Solved these Questions
Similar Questions
Two segments AC and BD bisect each other at O . Prove that ABCD is a parallelogram.
View SolutionIn a ABC median AD is produced to X such that AD=DX . Prove that ABXC is a parallelogram.
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
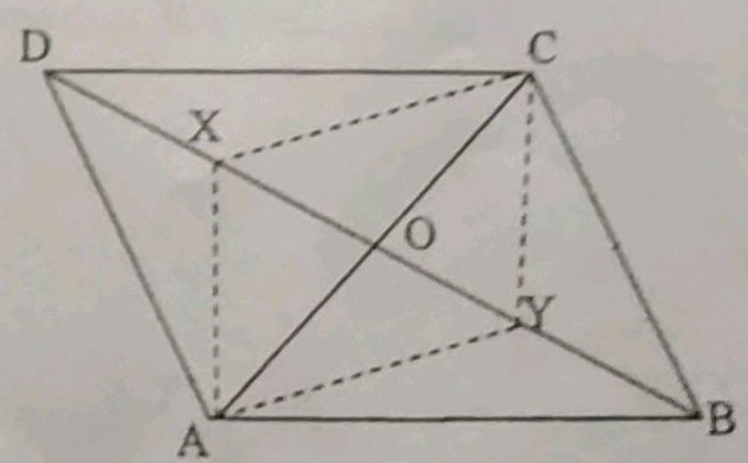
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram AB CD.
View SolutionIf the diagonals of a quadrilateral bisect each other at right angle, then the quadrilateral is a parallelogram (b) rectangle (c) rhombus (d) kite
View SolutionIf →a ,→b ,→c ,→d are the position vector of point A,B,C and D , respectively referred to the same origin O such that no three of these point are collinear and →a + →c = →b + →d , than prove that quadrilateral ABCD is a parallelogram.
View SolutionProve using vectors: The diagonals of a quadrilateral bisect each other iff it is a parallelogram.
View SolutionGiven the following statements :
A:If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
B: If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
Identify these as contrapositive or converse of each other.
View Solution
