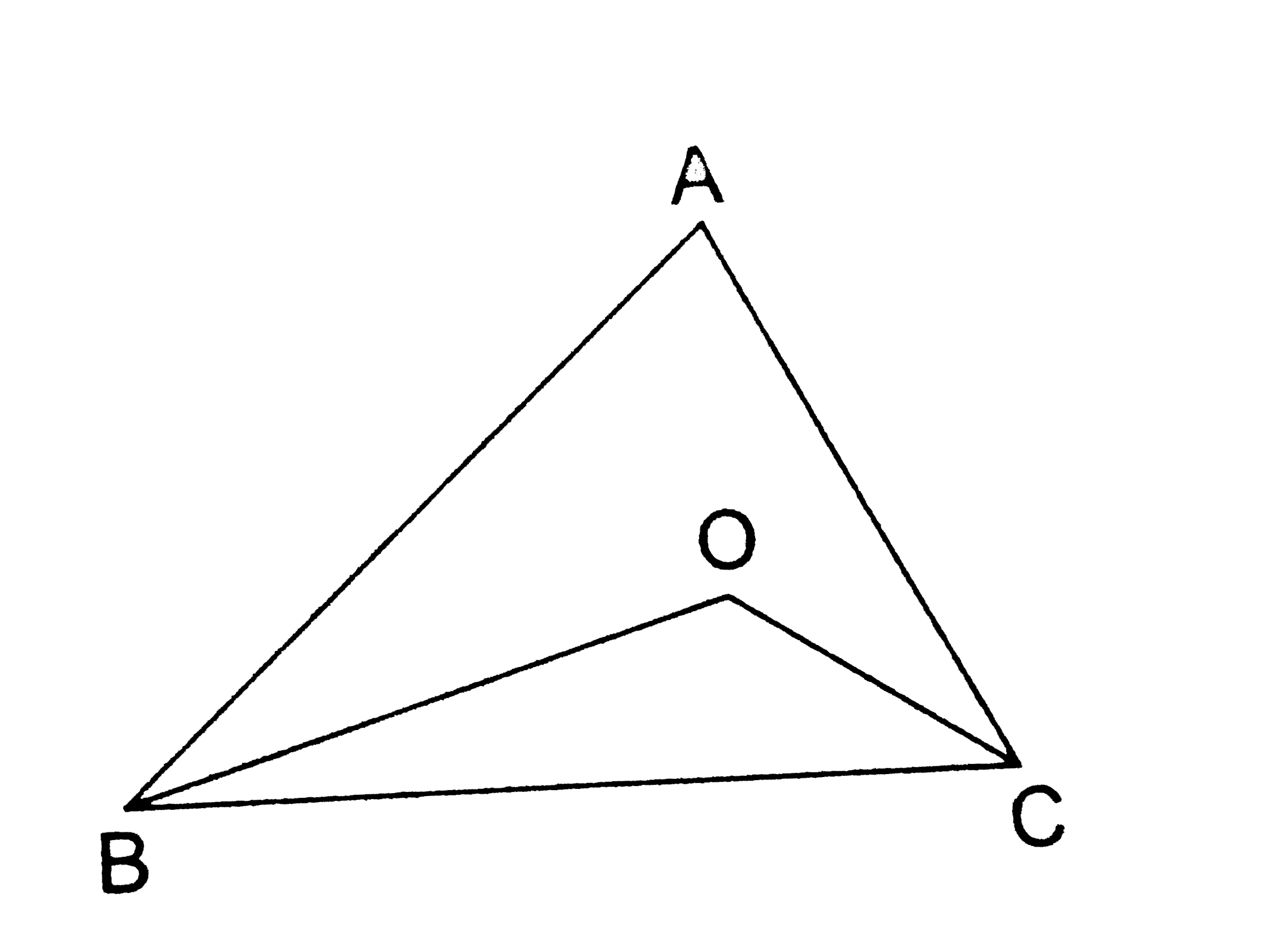
In a triangle ABC , OB and OC are the bisector of angle ∠B and ∠C respectively . ∠BAC=60∘ . The angle ∠BOC will be :
150∘
120∘
100∘
90∘
The correct Answer is:B
To find the angle ∠BOC in triangle ABC where OB and OC are the bisectors of angles B and C respectively, and ∠BAC=60∘, we can follow these steps:
1. Identify the Given Information:
- We have triangle ABC.
- ∠BAC=60∘.
- OB is the bisector of ∠B.
- OC is the bisector of ∠C.
2. Understand the Angles in Triangle:
- In any triangle, the sum of the angles is 180∘.
- Therefore, we can express ∠B+∠C as:
∠B+∠C=180∘−∠A=180∘−60∘=120∘
3. Let ∠B=b and ∠C=c:
- From the previous step, we have:
b+c=120∘
4. Using the Angle Bisector Theorem:
- The angle bisector divides the angle into two equal parts. Thus:
∠OBA=b2and∠OCA=c2
5. Finding ∠BOC:
- The angle ∠BOC can be calculated using the formula:
∠BOC=180∘−(∠OBA+∠OCA)
- Substituting the values:
∠BOC=180∘−(b2+c2)=180∘−b+c2
- Since b+c=120∘:
∠BOC=180∘−120∘2=180∘−60∘=120∘
6. Final Answer:
- Therefore, the angle ∠BOC is 120∘.
- We have triangle ABC.
- ∠BAC=60∘.
- OB is the bisector of ∠B.
- OC is the bisector of ∠C.
- In any triangle, the sum of the angles is 180∘.
- Therefore, we can express ∠B+∠C as:
∠B+∠C=180∘−∠A=180∘−60∘=120∘
- From the previous step, we have:
b+c=120∘
- The angle bisector divides the angle into two equal parts. Thus:
∠OBA=b2and∠OCA=c2
- The angle ∠BOC can be calculated using the formula:
∠BOC=180∘−(∠OBA+∠OCA)
- Substituting the values:
∠BOC=180∘−(b2+c2)=180∘−b+c2
- Since b+c=120∘:
∠BOC=180∘−120∘2=180∘−60∘=120∘
- Therefore, the angle ∠BOC is 120∘.
Similar Questions
Knowledge Check
In given triangle ABC ,OB and OC are bisectors of ∠Ba nd ∠C respectively then ∠BOC is equal to
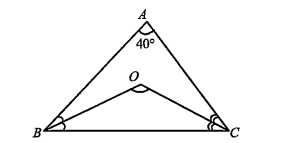 A70∘B110∘C140∘D80∘
A70∘B110∘C140∘D80∘In a triangle, with usual notations, the length of the bisector of angle A is
A2bcb+csinA2B2bcb+ccosA2Cabc2R(b+c)cosecA2D4Ab+ccosecA2In the given diagram of ΔABC,∠B=80∘,∠C=30∘ BF and CF are the angle bisectors of ∠CBDand∠BCE respectively. Find the value of ∠BFC :
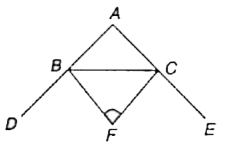 A110∘B50∘C125∘D55∘
A110∘B50∘C125∘D55∘
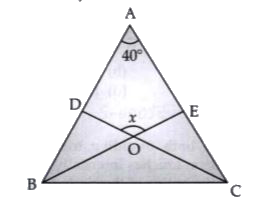
In the given figure , AB = AC , ∠BAC=40∘ , BE and CD are angle bisectors of ∠Band∠C respectively . If ∠DOE=x , the value of x is :
View SolutionBO and CO are external bisector of ∠B and ∠C of △ABC intersecting at O. If ∠A=60∘,∠ABC=70∘, Find ∠BOC
View SolutionBO and CO are external bisector of ∠B and ∠C of △ABC intersecting at O. If ∠A=60∘,∠ABC=70∘, Find ∠BOC
View SolutionIn △ABC the bisectors of ∠B and ∠C intersect at I if ∠A=70∘ then ∠BIC=…………..
View SolutionΔABC ,angle B external angle C meets at P ∠A=80 then ∠BPC = ?
View Solution