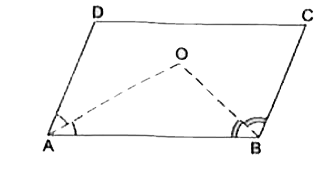
In the given figure, AB>AC. If BO and CO are the bisectors of ∠Band∠C respectively then
A
OB=OC
B
OB>OC
C
OB<OC
D
cannot be determined
Video Solution
Text Solution
The correct Answer is:B
AB>AC⇒∠C>∠B⇒12∠C>12∠B
⇒∠OCB>∠OBC⇒OB>OC.
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
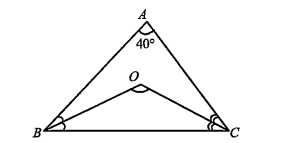
In given triangle ABC ,OB and OC are bisectors of ∠Ba nd ∠C respectively then ∠BOC is equal to
 A70∘B110∘C140∘D80∘
A70∘B110∘C140∘D80∘In a triangle ABC , OB and OC are the bisector of angle ∠B and ∠C respectively . ∠BAC=60∘ . The angle ∠BOC will be :
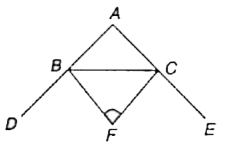
A150∘B120∘C100∘D90∘In the given diagram of ΔABC,∠B=80∘,∠C=30∘ BF and CF are the angle bisectors of ∠CBDand∠BCE respectively. Find the value of ∠BFC :
 A110∘B50∘C125∘D55∘
A110∘B50∘C125∘D55∘
In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively. Prove that ∠AOB=12(∠C+∠D).
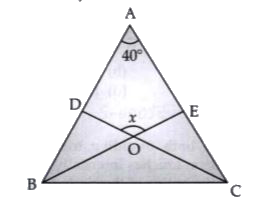
View SolutionIn the given figure , AB = AC , ∠BAC=40∘ , BE and CD are angle bisectors of ∠Band∠C respectively . If ∠DOE=x , the value of x is :
View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View SolutionIn the given figure DO and CO are the bisectors of ∠ADC and ∠BCD respectively. If ∠ADC=∠BCD=60∘ and ∠DAB=100∘ find
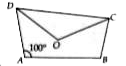
∠DOC and ∠ABC
View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OC
View Solution