ABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
Given ABCD is a qudrilateral such that AB||DC and AD = BC.
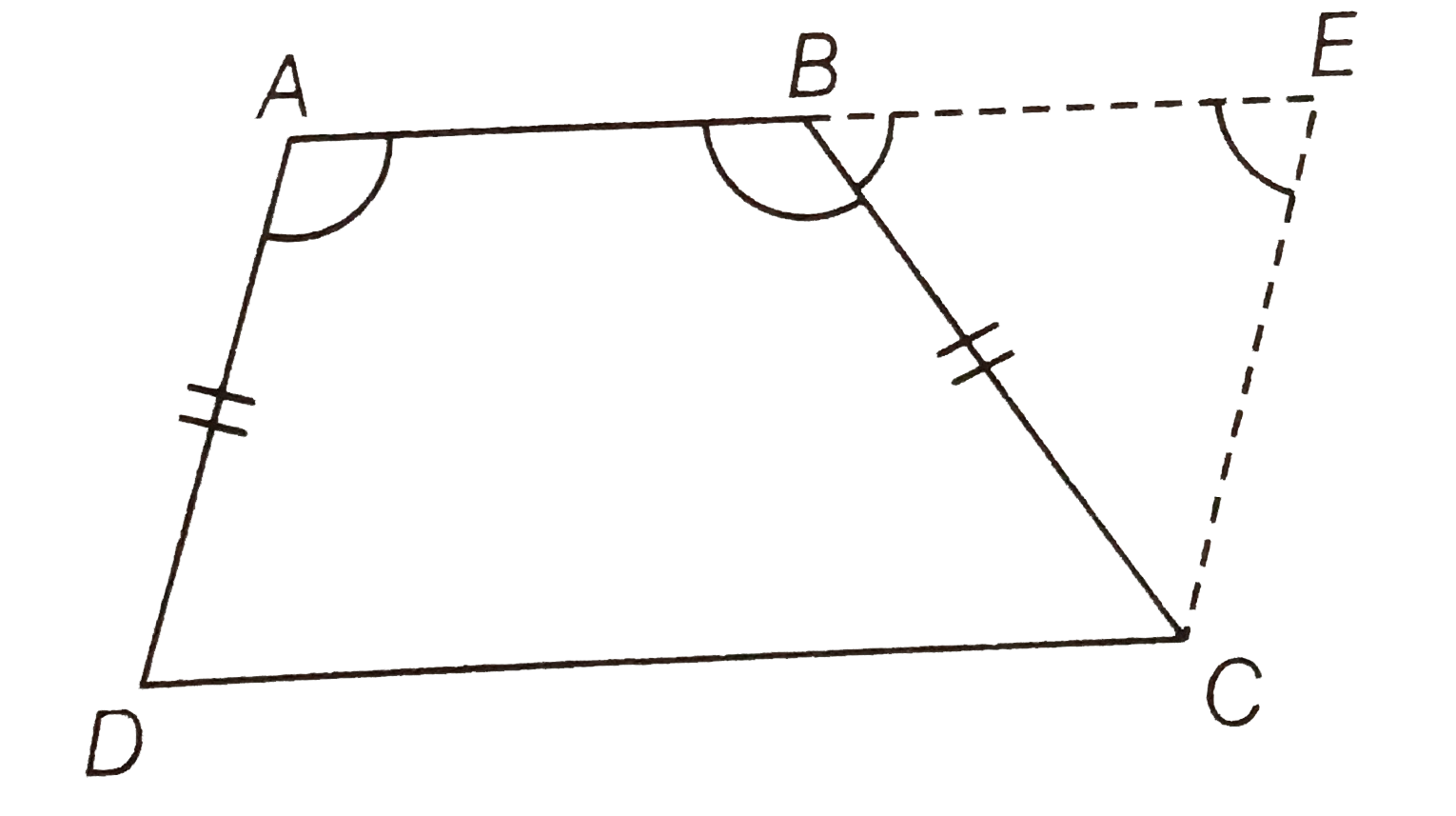
Construction Extend AB to E and draw a line CE parallel to AD.
Proof Since, AD||CE and transversal AE cuts them at A and E, respectively.
∴ ∠A+∠E=180∘ [since, sum of cointerior angles is 180∘]
⇒ ∠A=180∘−∠E ...(i)
Since, AB||CDandAD||CE
So, quadrilateral AECD is a parallelogram.
⇒ AD=CE⇒BC=CE [∵AD=BC,given]
Now, in ΔBCE
CE=BC [proved above]
⇒ ∠CBE=∠CEB ltBrgt [opposite angles of equal side are equal]
⇒ 180∘−∠B=∠E [∵∠B+∠CBE=180∘]
⇒ 180∘−∠E=∠B ...(ii)
From Eqs. (i) and (ii), ∠A=∠B Henced proved.
Topper's Solved these Questions
Similar Questions
If ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View SolutionIn quadrilateral ABCD, AB ||CD and AD= BC, prove that ∠A=∠B.
View SolutionABCD is a quadrilateral in which AB=CD and AD=BC. show that it is a parallelogram.
View SolutionABCD is a trapezium in which AB||CD and AD=BC (see figure). Show that
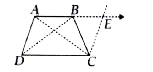
∠A=∠B
View SolutionIn the given figure ABCD is, ABCD is a quadrilateral in which AB∣∣DC and AD∣∣BC prove that ANGLEADC=ANGLEABC.

View SolutionOAOC=ODOB. Prove that ∠A=∠C and ∠B=∠D.
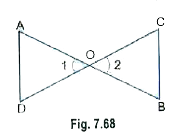
View SolutionABCD is a quadrilateral in which AB=BC and AD =CD ,Show that BD bisects boht the angle ABC and ADC
View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
∠A=∠B

View SolutionThe figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
View SolutionIn quadrilateral ABCD, BA = BC and DA = DC. Prove that BD bisects ∠ ABC as well as ∠ ADC.
View Solution